Usamos as frações em quase tudo na vida, mas operar com elas ainda é um grande desafio para a maioria das pessoas.
Muitos estudantes têm dificuldade de entender o que representa, quais os tipos de fração e quais as regras para cada tipo de operação, então neste post vamos explicar tudo para vocês!
O que é uma fração
A fração é uma representação de uma divisão em partes iguais onde comparamos a parte em relação ao todo, por exemplo:“Em quantas partes eu posso dividir igualmente uma pizza?”
Podemos dividir uma pizza em várias partes iguais, como por exemplo:
Como representar uma fração
Uma fração é composta pelo numerador (número de cima) e denominador (número debaixo).O numerador representa a PARTE.
O denominador representa o TODO.

Frações equivalentes
São frações que representam a mesma quantidade. Ou seja, elas podem estar sendo divididas em mais partes, porém representam a mesma quantidade, veja: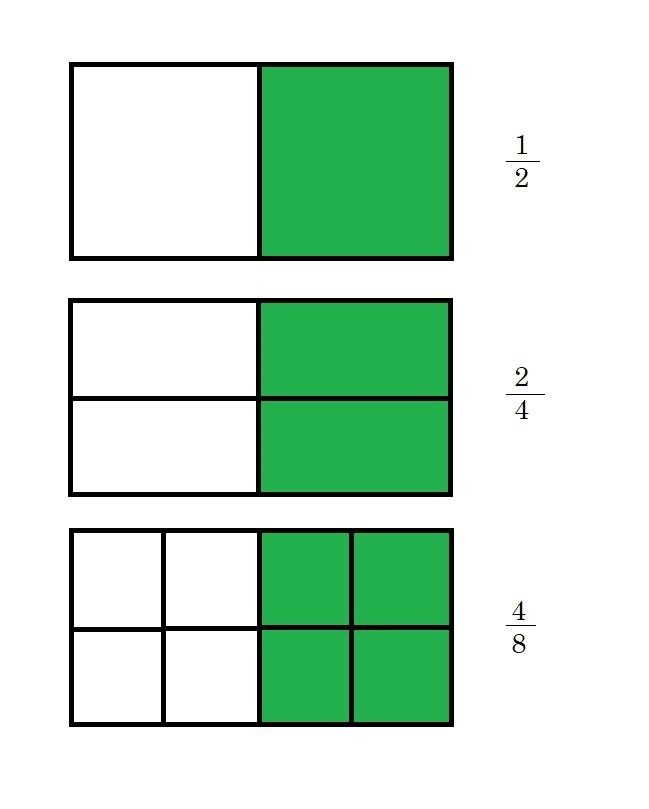
Algebricamente podemos encontrar as frações equivalentes multiplicando o denominador e o numerador por um mesmo número, ou simplificando ambos pelo mesmo número, veja:
1x2/3x2=2/6Temos que1/3e2/6são frações equivalentes, porque multiplicamos o numerador e o denominador da primeira fração por 2, que resultou na segunda fração.
40:20/100:20=2/5Temos que40/100e2/5são frações equivalentes, porque dividimos o numerador e o denominador da primeira fração por 20, que resultou na segunda fração.
Obs:Quando fazemos o processo do M.M.C. e depois fazemos “divide pelo debaixo e multiplica pelo de cima”, estamos na verdade encontrando frações equivalentes.Operações com frações
Adição e subtração de frações quando os denominadores são IGUAIS
Para somar ou subtrair frações com o mesmo denominador é fácil, só precisa fazer a conta na parte de cima (numeradores), veja:2/5+1/5=3/5
7/100-4/10=3/10
Obs:Nunca fazemos adição e subtração com os denominadores (parte debaixo).
Adição e subtração de frações quando os denominadores são DIFERENTES
Se você precisa somar ou subtrair frações com denominadores diferentes, primeiro você precisa entender como acha o M.M.C., para isso preparamos um vídeo especial para você:Para resolver a adição ou a subtração com frações, vamos precisar fazer M.M.C. entre os denominadores, e depois fazer a regrinha “divide pelo debaixo e multiplica pelo de cima”, porque precisamos encontrar as frações equivalentes deles, mas que tenham o mesmo denominador, vamos ver um exemplo pra entender:2/5+1/3
Os denominadores são 5 e 3, como são diferentes precisamos fazer o M.M.C. entre eles:
3,5 | 3 1,3 | 5 1,1 | 3x5
Agora é só multiplicar os fatores: 3 x 5 = 15, então o mmc(3, 5) = 15, e reescrevemos as frações equivalentes ambas com o denominador 15.
Para reescrever as frações em frações equivalentes podemos fazer por dois caminhos, veja:
Resolvendo por frações equivalentes
Podemos pensar em frações equivalentes, assim:2/5+?/15Por qual número multiplicamos o 5 para que ele resulte em 15? A resposta é o 3, então basta multiplicar o numerador por 3 também, resultando em 2 x 3 = 6.
2x3/5x3=6/15Fazemos o mesmo procedimento para a segunda fração:
1/3=?/15E a pergunta aqui é, qual é o número que multiplicado por 3 resulta em 15? E a resposta é, 5. Então, multiplicamos o numerador também por 5.
1x5/3x5=5/15Encontrado as frações equivalentes, basta fazer a conta:
2/5+1/3=6/15+5/15=11/15
Método Prático
Depois de ter feito o MMC, aplique a regra “divide pelo debaixo e multiplica pelo de cima”, assim, o resultado do MMC você divide pelo denominador, e o resultado disso você multiplica pelo numerador, veja:3x2/15:5+5x1/15:3=6/15+5/15=11/15Multiplicação com frações
Para multiplicar frações NÃO vamos fazer MMC, basta multiplicar o numerador com o numerador, e o denominador com o denominador: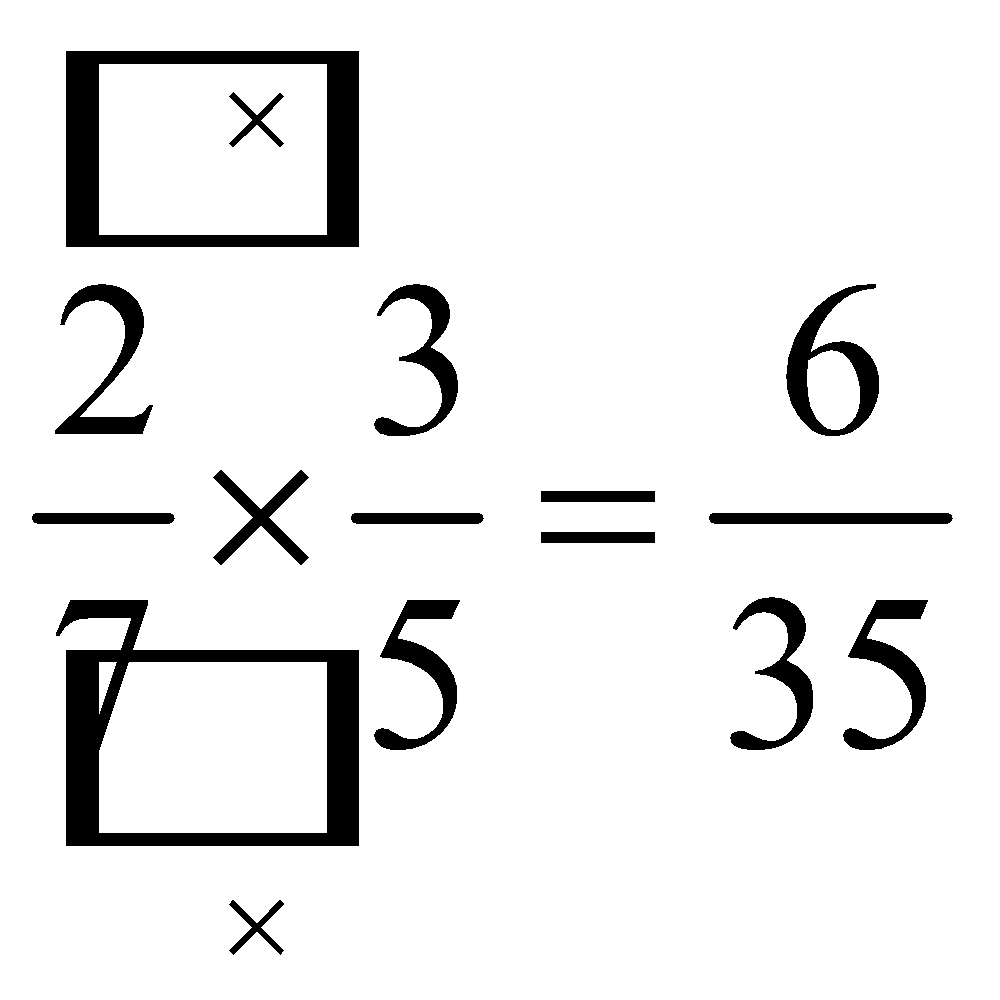
Divisão com frações
Assim como na multiplicação, na divisão também NÃO vamos fazer MMC, mas tem uma regrinha:“Inverta a segunda fração e a divisão vira uma multiplicação”
3/5÷7/4Vamos inverter a segunda fração e com isso a divisão passa a ser uma multiplicação:
3/5×4/7Agora é só multiplicar como aprendemos:
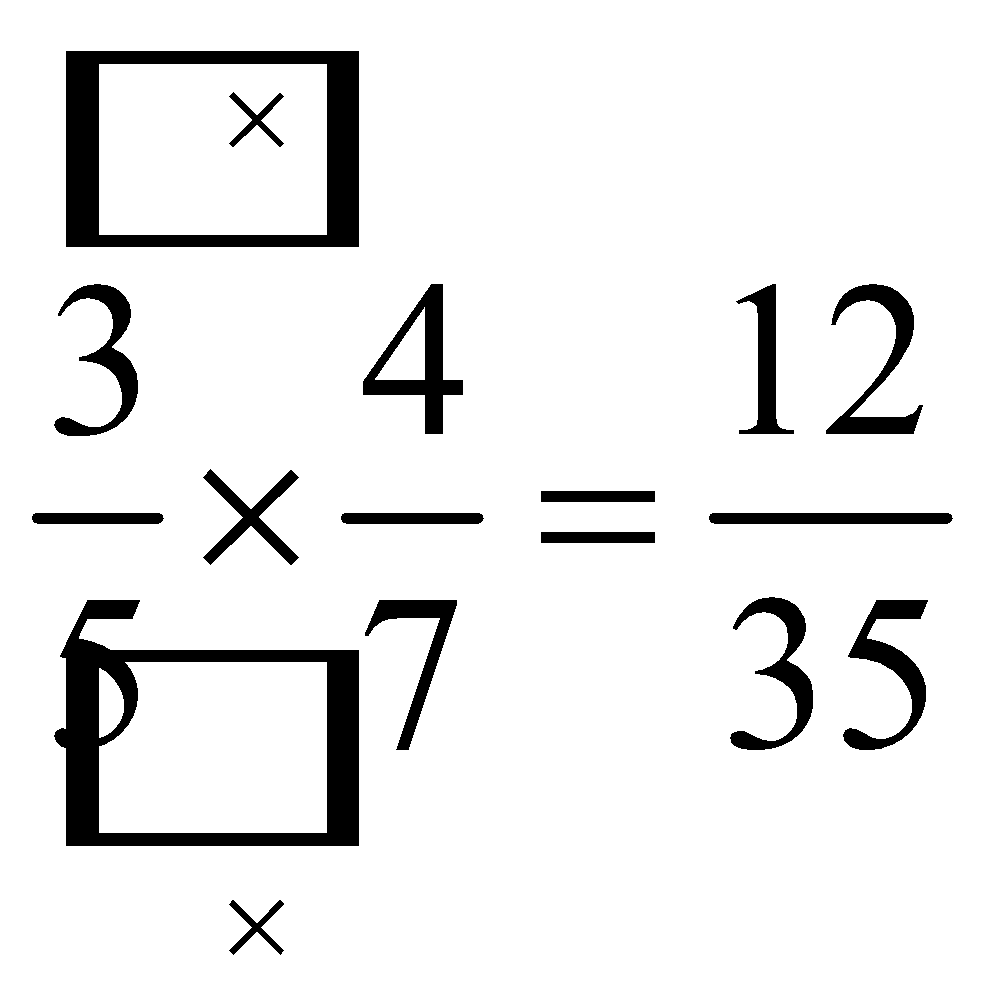
Veja mais sobre “Operações com frações” nesta aula com o Profº Gabriel Miranda:
Simplificação
Lembrando que sempre que for possível DEVEMOS simplificar as frações.“Mas, quando sei que devo simplificar?”
Resposta: sempre que o numerador e o denominador forem múltiplos, ou seja, que eu consigo dividir os dois por um mesmo número.
Exemplo:
15/30Os números 15 e 30 são múltiplos, consigo dividir ambos por: 3, 5, 6 e 15.
Se eu dividir por qualquer um dos números 3, 5 e 6, vou precisar simplificar novamente, veja:
15:5/30:5=3/6Porque os números 3 e 6 ainda são múltiplos, então DEVO simplificar até que eles não sejam mais múltiplos entre si:
15:5/30:5=3:3/6:3=1/2Agora, se você já saca de começo que o maior múltiplo já simplifica direto, basta dividir pelo maior múltiplo entre eles:
15:15/30:15=1/2Exercícios sobre tipos de fração
Agora é com você, vamos praticar alguns exercícios? Lembrando que temos o gabarito no final.
- Resolva as operações com frações a seguir e simplifique sempre que possível:
b)3/6-2/6=
c)2/7+1/3=
d)5/12-2/8=
e)5/4x3/6=
f)15/20x12/7
g)8/11÷3/5=
Legenda: Vamos pensar?
Gabarito:
a)3/5b)1/6
c)6+7/21=13/21
d)10-6/24=4: 4/24:4=1/6
e)15: 3/24:3=5/8
f)180: 20/140: 20=9/7
g)8/11x5/3=40/33
Gostou da nossa lista de exercícios sobre Tipos de fração? Aproveite para fazer questões antigas de provas do Enem e melhore sua preparação!
Conheça o nosso cursinho preparatório para o Enem e continue estudando com a ajuda de nossos professores.

