A Geometria espacial é muito importante para seu vestibular. Separamos um resumo das noções básicas que devem estar bem entendidas para o estudo mais aprofundado sobre esse tópico.
Geometria Espacial
1) Posição Relativa entre Retas
Retas Coincidentes
Duas retas são coincidentes quando são coplanares e possuem todos os pontos em comum.
Retas Paralelas
Duas retas são paralelas quando são coplanares e não possuem nenhum ponto em comum.
Retas Concorrentes
Uma reta é concorrente quando possuem apenas um ponto em comum, ou seja, se cruzam.
OBS: Duas retas que são concorrentes e formam entre si um ângulo de 90° são chamadas de Perpendiculares.
.jpg)
Perceba que elas se cruzam e também formam 90° entre si.
Retas Reversas
Duas retas são reversas quando não forem coplanares, ou seja, não forem do mesmo plano e não paralelas.
Um exemplo de pares de retas reversas.
2) Posição Relativa entre Reta e Plano
No estudo da geometria espacial usamos muito os conhecimentos entre planos e temos que relacionar muitos elementos que não estão presentes no mesmo plano. Assim, temos como relacionar a posição de uma reta e um plano qualquer pelas seguintes relações:
Reta Contida num Plano
Uma reta é dita contida num plano, quando todos os seus pontos fizerem parte a esse plano, ou seja, quando esse plano conter todos os pontos dessa reta.
.jpg)
Reta Paralela a um Plano
Uma reta é paralela a um plano quando eles não tiverem nenhum ponto em comum.
Perceba que a reta “r” é paralela tanto ao plano “α” quanto ao plano “β”.
Reta Secante ou Concorrente ao Plano
Uma reta é secante, ou concorrente, quando ela possui apenas um ponto em comum com o plano.
OBS: Uma reta é Perpendicular ao plano quando formar 90° com o plano concorrente a ela.
3) Posição relativa entre Planos
Podemos analisar, também, a posição relativa entre planos no espaço. São infinitos planos que podem se cruzar ou não, gerando tais relações:
Planos Paralelos
Dois planos são paralelos quando não possuírem nenhum ponto em comum.
.jpg)
Perceba que a reta “r” contida no plano alfa é paralela à reta “s” contida no plano Beta.
Panos Secantes
Dois planos serão secantes quando a interseção entre eles for uma reta.
perceba que a reta “r” é a interseção entre os planos alfa e beta e que “P” é um ponto em comum entre eles pois pertence à reta.
OBS: Dois planos serão Perpendiculares quando eles formarem 90° entre si.
Planos Coincidentes
Dois planos serão coincidentes quando possuem todos os seus pontos em comum.
.jpg)
Exercícios
1) (G1 – cftmg 2014) A figura a seguir representa uma cadeira onde o assento é um paralelogramo perpendicular ao encosto.
A partir dos pontos dados, é correto afirmar que os segmentos de retas
a) CD e EF são paralelos.
b) BD e FJ são concorrentes.
c) AC e CD são coincidentes.
d) AB e EI são perpendiculares.
2) (ENEM)
João propôs um desafio a Bruno, seu colega de classe: ele iria descrever um deslocamento pela pirâmide a seguir e Bruno deveria desenhar a projeção desse deslocamento no plano da base da pirâmide.
O deslocamento descrito por João foi: mova-se pela pirâmide, sempre em linha reta, do ponto A ao ponto E, a seguir do ponto E ao ponto M, e depois de M a C. O desenho que Bruno deve fazer é
a)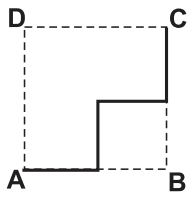 
b)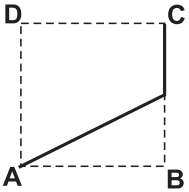 
c)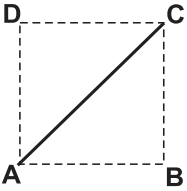 
d)
e)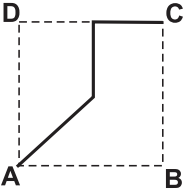 
3) (UFF) Marque a opção que indica quantos pares de retas reversas são formados pelas retas suportes das arestas de um tetraedro.
a) Um par.
b) Dois pares.
c) Três pares.
d) Quatro pares.
e) Cinco pares.
Gabarito
1) A
2) C
3) C
Colaboração: Allan Pinho
