Área(s) de Conhecimento do ENEM: Combinatória – Princípios básicos
Competência relacionada: 1
Construir significado para os números naturais, inteiros, racionais e reais
Habilidade relacionada: H2
Identificar padrões numéricos ou princípios de contagem.
Análise combinatória, sem dúvidas, é um dos assuntos que causam mais terror nos candidatos de vestibular. Mas, você sabia que ela pode não ser tão assustadora assim? Perceba como os vestibulares também cobram os princípios básicos de análise combinatória.
1) Cesgranrio – 2000
Uma partícula deve ir do ponto P ao ponto M, percorrendo a menor distância possível, deslocando-se somente por sobre as linhas da figura e com velocidade média de 2 cm/s. Como exemplo, temos, a seguir, uma representação de um desses caminhos. Quantos são os possíveis caminhos que tal partícula poderá percorrer?
a) 256 b) 128 c) 120 d) 70 e) 56
Resolução:
Utilizando as letras D, para direita e C, para cima, o caminho mostrado pode ser descrito como DCCCDCDD. Outro caminho poderia ser o mostrado na outra figura.
Este caminho seria: CCDCCDDD. Repare que independente do caminho, há 4 C’s e 4 D’s em posições trocadas. Podemos interpretar essa situação como “anagramas” e calcular de quantas formas podemos dispor essas letras.
Temos:
Perceba que essa permutação houve uma repetição de elementos, eram 8 elementos, com 4 “c” e 4 “d” repetindo, por isso os dois 4! no denominador.
Como eu errava esse tipo de coisa?!
2) ENEM – 2012
O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.
Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a
brincadeira é encerrada.
O diretor sabe que algum aluno acertará a resposta porque há:
a) 10 alunos a mais do que possíveis respostas distintas.
b) 20 alunos a mais do que possíveis respostas distintas.
c) 119 alunos a mais do que possíveis respostas distintas.
d) 260 alunos a mais do que possíveis respostas distintas.
e) 270 alunos a mais do que possíveis respostas distintas.
Resolução:
O número de respostas distintas deve ser calculado através do princípio fundamental da contagem, o princípio multiplicativo. A resposta é composta pelo nome do objeto “e” personagem “e” cômodo da casa. Quando o conectivo “e” é utilizado, o número de possibilidades deve ser multiplicado para encontrar o total de possibilidades da resposta. Caso o conectivo fosse o “ou” seria utilizado o princípio aditivo da contagem. O total de possibilidades é de 5 para o objeto, 6 para o personagem e 9 para o cômodo da casa. Utilizando o princípio multiplicativo, temos 5x6x9=270 possibilidades de respostas. Como são 280 alunos, são 280 – 270=10 alunos a mais que as possibilidades de resposta. Logo, a resposta é letra A!!!
ahh o Enem… zzZ
3) UERJ – 2009
Considere a situação abaixo:
Essa solução está errada. Apresente a solução correta.
Solução:
Nesta situação, há seis possibilidades de se escolher uma mulher e, para cada uma dessas escolhas, existem seis possibilidades de se escolher um homem.
Portanto, o número de maneiras distintas de se formar um casal é dado por:
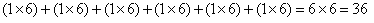
Mas era só isso?! =O
4) OBMEP – 2011
Cada uma das placas das bicicletas de Quixajuba contém três letras.
A primeira letra é escolhida dentre os elementos do conjunto A={G, H, L, P, R}, a segunda letra é escolhida dentre os elementos do conjunto B={M, I, O} e a terceira letra é escolhida dentre os elementos do conjunto C={D, U, N, T}.
Devido ao aumento no número de bicicletas da cidade, teve-se que expandir a quantidade de possibilidades de placas. Ficou determinado acrescentar duas novas letras a apenas um dos conjuntos ou uma letra nova a dois conjuntos.
Qual o maior número de novas placas que podem ser feitos, quando se acrescentam as duas novas letras?
Solução:
Inicialmente, é possível fazer o emplacamento de 5 × 3 × 4 = 60 bicicletas. Vamos analisar as duas situações possíveis:
– Aumentamos duas letras num dos conjuntos. Com isso, podemos ter:
Assim, com a modificação mostrada, o número de novas placas é no máximo 100-60=40.
– Aumentar uma letra em dois dos conjuntos. Com isso, podemos ter:
Neste caso, o número de placas novas também é no máximo 40.
Seus problemas descomplicaram-se?
