Você sabe qual é o presente perfeito para o seu namorado ou sua namorada? Descubra aqui e ainda aprenda sobre poliedros para arrasar na sua prova de matemática!
Com o dia dos namorados chegando, muitos namorados sempre entram naquele dilema sobre “O QUE VOU DAR DE PRESENTE PARA ELE/ELA?”. Muitos homens e mulheres apelam para as jóias, outros para bombons, ou simplesmente fazem um jantar caseiro a luz de velas. Mas você sabe como se preocupar com seu relacionamento e mesmo assim não perder o foco no vestibular? Entenda agora!
Tenham namorados românticos sempre…
1) As jóias e os poliedros convexos
Você já sabe que um poliedro é um sólido formado apenas por linhas não curvas, onde temos as faces em formas de polígonos. Assim como os polígonos, os poliedros podem ser convexos ou não convexos. Mas como você vai saber diferenciar? Pense nas jóias! Na maioria, temos elas na forma de um poliedro convexo.
Um poliedro é convexo se qualquer reta (não paralela a nenhuma de suas faces) o corta em, no máximo, dois pontos, ou seja, quando traçamos uma reta qualquer que corte esse poliedro, ela não pode interceptá-lo em mais de dois pontos:
Perceba que todos esses poliedros são convexos
Perceba que na figura da esqueda temos um poliedro convexo e na figura da direita temos um poliedro não convexo pois uma reta o corta em mais de dois pontos.
Lembrando que a RELAÇÃO DE EULER vale apenas para poliedros convexos. Essa lei nos diz que:
V + F = A + 2
Sendo V a quantidade de vértices, F a quantidade de faces e A a quantidade de arestas desse polígono.
Aí você ganha aquele diamante…
2) Cubo mágico e os poliedros regulares
Para você, que não sabe mais o que fazer para tirar o seu grande amor de dentro do quarto, mas ele(a) não larga a tela do Descomplica, não pára de estudar, um conselho: crie um super desafio para ele se ligar mais em você! E que tal você fazer isso dando um cubo mágico de fotos românticas de vocês?
Existem diversos tipos de puzzles como este, mas o que eles têm com isso tudo? Todos eles são poliedros regulares!
Existem muitos tipos diferentes desses puzzles
Um polígono é regular quando suas faces são polígonosregulares, cada um com o mesmo número de lados e, para todo vértice, converge um mesmo número de arestas.
Ahh, mano… não..
3) Caleidociclo e Soma dos ângulos das faces
Caleidociclo, pra quem não sabe, é um origami que formam ciclos de imagens. Esse origami é construído a partir de seis tetraedros e é um excelente presente fofinho para sua amada ou amado.
Para a construção dessa engenhoca, devemos usar o seguinte molde, de onde conseguimos formar os tetraedros:
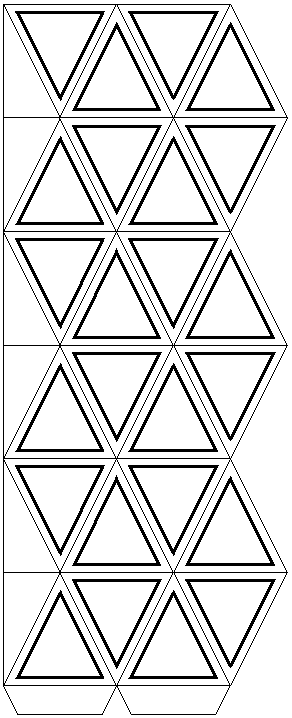
Para fazer o recorte, devemos perceber a angulação entre as arestas desse futuro tetraedro, assim, podemos facilmente perceber apenas somando esses ângulos sobre a soma dos ângulos das faces de um tetraedro.
Essa soma é sempre dada pela fórmula:
S = ( V – 2 ).360°
Isso é muito irado!
