Conheça mais sobre o triângulo retângulo e as relações que podemos ter entre seus lados e segmentos e chegaremos a 5 relações métricas. Confira!
Trabalharemos usando como referência o triângulo ABC abaixo: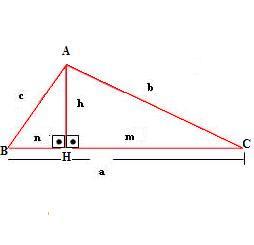
Com "a" sendo a hipotenusa, "b" e "c" sendo os catetos, "h" sendo a altura e "m" e "n" sendo as projeções dos catetos sobre a hipotenusa.
1) a.h = b.c
Começaremos pela semelhança dos triângulos ABC e HBA.∆ABC ~ ∆HBA
c/h = a/bMultiplicando cruzado, temos:
a.h = b.c
2) b² = am
A partir da semelhança entre os triângulos ABC e HAC, conseguimos a seguinte relação:∆ABC ~ ∆HAC
b/m = a/bMultiplicando cruzado, temos:
b² = a.mOu seja, o quadrado de um dos catetos é igual ao produto da hipotenusa por sua projeção. Isso também valerá para o outro cateto como veremos a seguir.
3) c² = a.n
Agora, faremos a semelhança entre os triângulos ABC e o triângulo HBA, assim, temos a seguinte relação:∆ABC ~ ∆HBA
c/n = a/cMultiplicando cruzado, temos:
c² = a.n
4) O teorema de Pitágoras
Sim, o Teorema de Pitágoras também é uma relação métrica. E ele aparece a partir dessas duas primeiras relações, perceba:b² = a.mSomando as duas equações, temos:c² = a.n
c² + b² = a.m + a.nColocando "a" em evidência, temos:
c² + b² = a.(m+n)Porém, m+n = a, observe a primeira figura! Assim, temos o famoso:
c² + b² = a²
5) h² = m.n
A última relação é proveniente da semelhança dos triângulos HBA e HAC, assim, temos:
∆HBA ~ ∆HAC
h/n = m/hMultiplicando cruzado, temos:
h² = m.n
Exercícios
1) Em um mapa, as cidades A, B e C são os vértices de um triângulo retângulo e o ângulo reto está em A. A estrada AB tem 80 km e a estrada BC tem 100 km. Um rio impede a construção de uma estrada que ligue diretamente a cidade A com a cidade C. Por esse motivo, projetou-se uma estrada saindo de A e perpendicular à estrada BC, para que ela seja a mais curta possível. Qual será o comprimento da estrada que será construída?
2) (UERJ) Na figura a seguir, estão representados o triângulo retângulo ABC e os retângulos semelhantes I, II e III, de alturas h1, h2 e h3 respectivamente proporcionais às bases ![]() ,
, ![]() e
e ![]() .
.
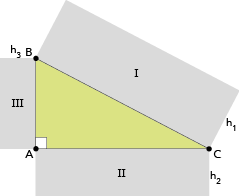
Se ![]() = 4 m e
= 4 m e ![]() = 3 m, a razão
= 3 m, a razão![]() é igual a:
é igual a:
a) 5
b) 4
c) 3
d) 2
3) (UERJ)Para construir a pipa representada na figura abaixo pelo quadrilátero ABCD, foram utilizadas duas varetas, linha e papel.

As varetas estão representadas pelos segmentos e
. A linha utilizada liga as extremidades A, B, C e D das varetas, e o papel reveste a área total da pipa.
Os segmentos e
são perpendiculares em E, e os ângulos
e
são retos.
Se os segmentos e
medem, respectivamente, 18 cm e 32 cm, determine o comprimento total da linha, representada por
+
+
+
.
Gabarito
1) 48 km2) A
3) 140 cm

