Você sabe tudo sobre triângulos?
 Uma das principais formas geométricas estudadas na nossa matemática e muito cobrada no ENEM é o triângulo. Como sabemos, o triângulo é formado por 3 vértices, 3 ângulos e 3 lados. Mas você sabe tudo sobre essa figura tão importante no estudo da geometria?
Uma das principais formas geométricas estudadas na nossa matemática e muito cobrada no ENEM é o triângulo. Como sabemos, o triângulo é formado por 3 vértices, 3 ângulos e 3 lados. Mas você sabe tudo sobre essa figura tão importante no estudo da geometria?DEPOIS DE DESCOBRIR TUDO SOBRE TRIÂNGULOS, CONFIRA NOSSO GABARITO DO ENEM 2015!
Classificação de um triângulo
Classificação quanto aos ângulos
- Triângulo acutângulo: possui todos os ângulos com medidas menores que 90º.
- Triângulo retângulo: possui um ângulo com medida igual a 90º.
- Triângulo obtusângulo: possui um ângulo obtuso, maior que 90º.
 Respectivamente: acutângulo, retângulo e obtusângulo[/caption]Classificação quanto aos lados
Respectivamente: acutângulo, retângulo e obtusângulo[/caption]Classificação quanto aos lados- Triângulo equilátero: possui os três lados com medidas iguais.
- Triângulo isósceles: possui dois lados com medidas iguais.
- Triângulo escaleno: possui os três lados com medidas diferentes.
 Respectivamente: equilátero, isósceles e escaleno[/caption]
Respectivamente: equilátero, isósceles e escaleno[/caption]Condição de existência e ângulos de um triângulo
.jpg)
- a < b + c
- b < a + c
- c < a + b
Área de um triângulo
É muito comum, no ENEM, que caia na sua prova uma questão sobre áreas, principalmente de triângulos. A área de um triângulo pode ser calculada de algumas formas.Produto da base pela altura
A área de um triângulo é a metade do produto da medida da sua altura pela medida da sua base. Assim, pode ser calculada pela fórmula:
Trigonometria

Semiperímetro (Fórmula de Heron)
Outra maneira de calcular sua área é através do Teorema de Heron, também conhecido como fórmula do semi-perímetro:Raio circunscrito
Há ainda a fórmula da área do triângulo em função das medidas dos lados a, b e ce do raio r da circunferência que circunscrita esse triângulo. A fórmula é demonstrada pela lei dos senos: OBS: Num triângulo equilátero, em que temos todos os lados e todos os ângulos iguais, temos que a área pode ser escrita com uma fórmula específica:
OBS: Num triângulo equilátero, em que temos todos os lados e todos os ângulos iguais, temos que a área pode ser escrita com uma fórmula específica:Semelhança de triângulos
Caso AA (Ângulo, Ângulo)
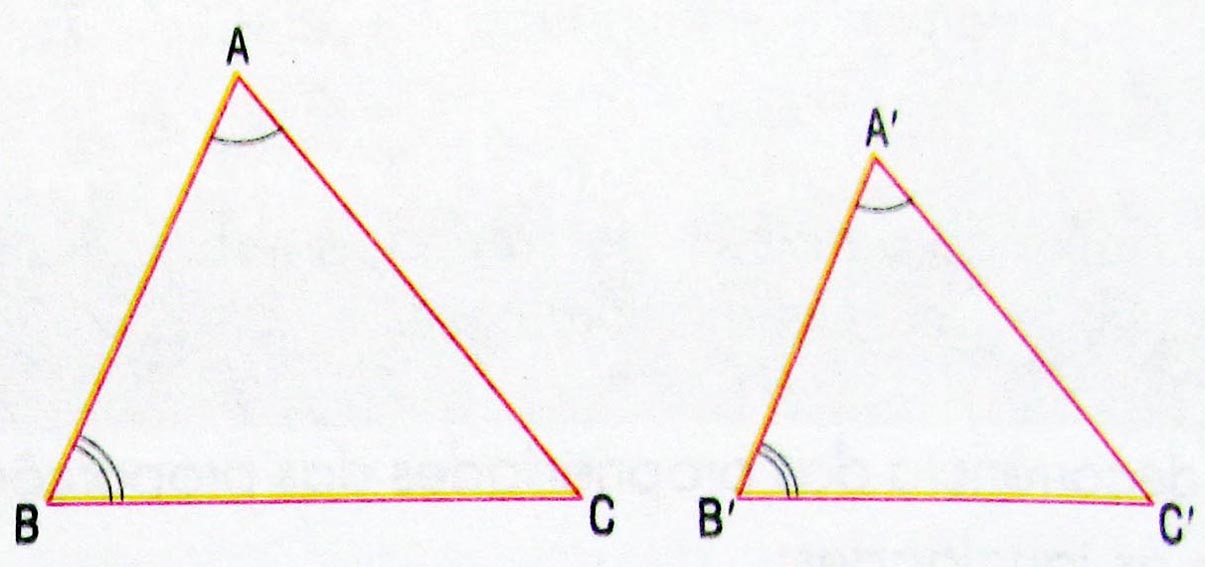
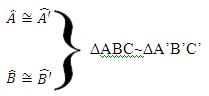
Caso LLL (Lado, Lado, Lado)

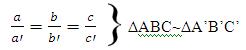
Caso LAL (Lado, Ângulo, Lado)
Se dois triângulos possuírem um ângulo congruente formado entre dois lados de medidas proporcionais, os dois triângulos são semelhantes.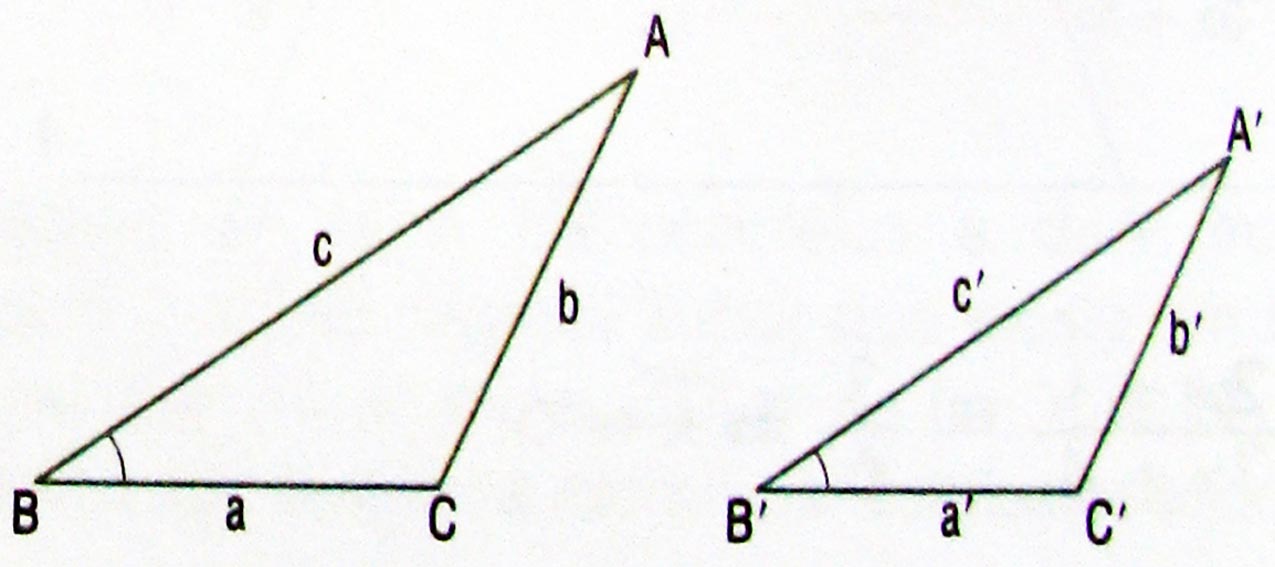
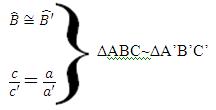
Triângulo Retângulo
É todo triângulo que possui um de seus ângulos retos. Podemos estabelecer uma relação entre seus lados – sendo seu maior lado, oposto ao ângulo de 90°, chamado de hipotenusa –, enquanto que os outros dois lados são chamados de catetos. Essa relação é o famoso Teorema de Pitágoras, veja:.jpg) Daí, temos que o Teorema de Pitágoras diz que:
Daí, temos que o Teorema de Pitágoras diz que:c² = a² + b²
Trigonometria no triângulo retângulo
Num triângulo retângulo, podemos estabelecer relações entre seus lados e seus ângulos; essas são chamadas de razões trigonométricas. São elas:- Seno: é a razão entre a medida do cateto oposto a esse ângulo e a medida da hipotenusa.
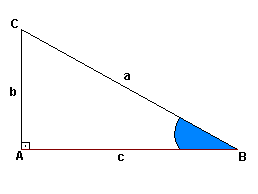
Sen(B) = b/aSen(C) = c/a
- Cosseno: é a razão entre a medida do cateto adjacente a esse ângulo e a medida da hipotenusa.

Cos(B) = c/aCos(C) = b/a
- Tangente: é a razão entre a medida do cateto oposto e a medida do cateto adjacente a esse ângulo.

Tg(B) = b/cTg(C) = c/b
EXERCÍCIOS
1. (UNESP) A sombra de um prédio, num terreno plano, numa determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m.GABARITO
1. AVimos que esses triângulos retângulos formados são semelhantes; assim, montando a semelhança, temos:x/15 = 5/33x = 75x = 75/3x = 25 m2. Temos que, num triângulo retângulo, o seno de um ângulo agudo é dado pela razão entre o cateto oposto a esse ângulo e a hipotenusa desse triângulo. Assim:
sen30 = x/51/2 = x/52x = 5x = 5/2x = 2,5Este é um dos catetos.Sabemos que o cosseno de um ângulo agudo é dado pela razão entre o cateto adjacente a esse ângulo e a hipotenusa. Assim:
cos30 = y/5√3/2 = y/55√3 = 2yy = 5√3/2Este é o outro cateto.3) Temos que A = 16√3 cm². Assim:
L²√3 / 4 = 16√3L²√3 = 4.16√3L²√3 = 64√3L² = 64√3 /√3L² = 64L = 8 cm

