
Agora você vai entender de fato a descrição dos movimentos planetários com apenas três leis.
As famosas três leis de Kepler são leis que regem os movimentos planetários. Foram definidas pelo brilhante matemático e astrônomo alemão Johannes Kepler (1571 - 1630). Kepler descobriu que suas observações astronômicas seguiam três leis matemáticas relativamente simples. Suas conclusões desafiavam a astronomia e a física aristotélica e ptolomaica.
Afirmar que a Terra se movia, trocar uma forma de trajetória elíptica em vez de epiciclos (trajetórias circulares), provar que as velocidades dos planetas variavam, não foi uma tarefa fácil. Todos esses conhecimentos batiam de frente com o que a igreja católica pregava. No entanto, suas ideias estavam coerentes com a razão e a observação dos fatos. Seu modelo heliocêntrico substituiu não só apenas um modelo geocêntrico ultrapassado, mas uma nova maneira de ser compreender o mundo.

História e o embate geocêntrico e heliocêntrico
A teoria do universo geocêntrico ou geocentrismo é o modelo cosmológico mais antigo. Na antiguidade era raro quem discordasse dessa visão; e entre os filósofos que defendiam esta teoria, o mais conhecido era Aristóteles. Foi o matemático e astrônomo grego Ptolomeu (90 -168 d.C.) que, na sua obra “Almagesto", deu a forma final a esta teoria, que se baseia na hipótese de que o planeta Terra estaria fixo no centro do Universo com os corpos celestes, inclusive o Sol, girando ao seu redor.

A visão geocêntrica predominou no pensamento humano até o resgate, feito pelo astrônomo e matemático polonês N. Copérnico (1473-1543), de uma hipótese igualmente antiga: a hipótese heliocêntrica. Tal ideia fora, na verdade, criada pelo astrônomo grego Aristarco de Samos (310-230 a.C.). Por isso, foi um resgate, ainda mais que as antigas escrituras foram ocultadas pela igreja católica, sendo muitas queimadas pela Inquisição.
Esse sistema geocêntrico se mostrou muito favorável a teologia da Igreja Católica e, por isso mesmo, ele sobreviveu praticamente intacto por treze séculos. O geocentrismo só veio a ser efetivamente contestado a partir do julgamento do astrônomo e físico italiano Galileu Galilei, já no século XVII. E de fato, foi apenas no século XVIII que o estudo mais aprofundado da mecânica e dos corpos celestes demonstrou definitivamente que o geocentrismo havia sido um engano perpetuado por mais de milênio.
Embora a ideia não lhe fosse original, Copérnico foi o primeiro a estabelecer um modelo heliocêntrico aceitável. Contudo, com precisão empírica não muito melhor do que a fornecida por Ptolomeu, seu sistema ainda deixava muito a desejar. O modelo foi apreciavelmente melhorado pelo astrônomo alemão Kepler, que, debruçado sobre meticulosos dados coletados por Tycho Brahe ao longo de 20 anos de sua vida, abandonou a ideia de órbitas circulares e construiu um modelo centrado no sol com os planetas revolvendo em órbitas elípticas ao redor desse.
As Leis de Kepler encontram-se publicadas em “Astronomia Nova" (1609). A precisão empírica mais acurada levou o seu modelo a ser rapidamente aceito entre os eruditos, e entre estes, coube ao grande físico inglês Isaac Newton a responsabilidade de estabelecer a razão física de ser do modelo estabelecido por Kepler: a gravidade. A lei da gravitação universal foi publicada, juntamente com as três leis da dinâmica, em “Princípios Matemáticos da Filosofia Natural” (1687).
Há muito se sabe que o Sol não é o centro do universo e sim apenas mais uma estrela entre tantas outras. Ainda assim, as regras primariamente encontradas no modelo de universo heliocêntrico, baseado na gravitação universal, são até hoje utilizadas na exploração espacial.
Por outro lado, o modelo Ptolomaico não encontra lugar hoje no meio científico a não ser nos livros de história da ciência. E embora em desuso, o modelo de Ptolomeu, em termos de descrição empírica, é razoavelmente condizente com o que de fato se observa quando se está em um referencial atrelado à Terra - o referencial naturalmente assumido pelo senso comum (o que justificava à época o sucesso do modelo). É a ciência se renovando a cada dia!
1. As leis de Kepler
Em 1596, Kepler publicou Mysterium Cosmographicum, onde expôs argumentos favoráveis às hipóteses heliocêntricas. Em 1609 publicou “Astronomia Nova… De Motibus Stellae Martis”, onde apresentou as três leis do movimento dos planetas, que hoje levam seu nome. Vejamo-las:
1.1. Primeira Lei de Kepler: lei das órbitas elípticas
“O planeta em órbita em torno do Sol descreve uma elipse em que o Sol ocupa um dos focos”.
Esta lei definiu que as órbitas não eram circunferências, como se supunha até então, mas sim elipses. A distância de um dos focos até o objeto, mais a distância do objeto até o outro foco, é sempre igual não importando a localização do objeto ao longo da elipse.

1.2. Segunda Lei de Kepler: lei das áreas
“A linha que liga o planeta ao Sol (raio vetor) varre áreas iguais em tempos iguais”.
Esta lei determina que os planetas se movem com velocidades diferentes, dependendo da distância a que estão do Sol. Importa-nos apenas dois pontos:
Periélio: é o ponto mais próximo do Sol, onde o planeta orbita mais rapidamente.
Afélio: é o ponto mais afastado do Sol, onde o planeta move-se mais lentamente.

1.3. Terceira Lei de Kepler: lei dos períodos
“Os quadrados dos períodos de translação dos planetas são proporcionais aos cubos dos semi-eixos maiores de suas órbitas”.
Sendo T o período de revolução (ano do planeta) e R o semi-eixo maior da órbita de um planeta, tem-se:
T²/R³ = constante
Esta lei indica que existe uma relação entre a distância do planeta e o período de translação (tempo que ele demora para completar uma revolução em torno do Sol). Portanto, quanto mais distante estiver do Sol mais tempo levará para completar sua volta em torno desta estrela. Veja novamente a figura da primeira lei de Kepler neste artigo e perceba as diferentes trajetórias e se pergunte quem demoraria mais tempo para dar uma volta completa em torno do Sol.
2. Exercícios aplicado
Certa vez o Enem (2012) perguntou sobre a causa da forma da trajetória do planeta Marte registrada na seguinte ilustração:
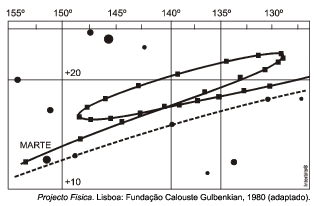
Primeiramente devemos lembrar que a característica que permite identificar um planeta no céu é o seu movimento relativo às estrelas fixas. Se observarmos a posição de um planeta por vários dias, verificaremos que sua posição em relação às estrelas fixas se modifica regularmente.
Outro ponto importante a ser levado em consideração é que apesar de as órbitas serem elípticas, elas na verdade são quase circulares. Assim, é muito comum que as questões tratam as órbitas dos planetas como sendo circulares. Isso facilita muito, pois assim podemos verificar que a força gravitacional será a resultante centrípeta das forças que atuam sobre o corpo. Na verdade, só há uma força: a força gravitacional. E por somente ela existir, ela atuará como resultante centrípeta.
Com essa suposição, chega-se a conclusão que a velocidade v de órbita de um planeta em torno de uma estrela, no caso o Sol (considerado fixo), será:
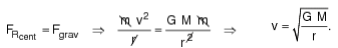
Essa expressão final evidencia que a velocidade orbital é inversamente proporcional à raiz quadrada do raio da órbita. Como a Terra está mais próxima do Sol que Marte, sua velocidade orbital é maior, possuindo, em consequência, também maior velocidade angular e menor período.
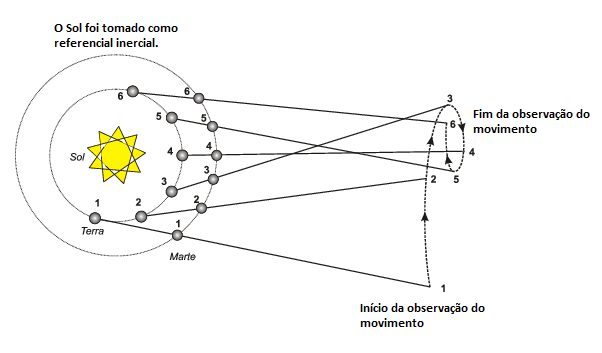
A ilustração acima revela seis posições da Terra e as seis correspondentes posições de Marte, bem como a trajetória de Marte para um observador situado na Terra. Os intervalos de tempo entre duas posições consecutivas são, aproximadamente, iguais. Note que devido à maior velocidade orbital da Terra, da posição 1 até a 3, Marte parece avançar, de 3 a 5 ele parece regredir, tornando a avançar de 5 a 6. Aliás, esse fenômeno foi um dos grandes argumentos para que o heliocentrismo de Copérnico superasse o geocentrismo de Ptolomeu.
Portanto, voltemos para a pergunta. Qual a causa da trajetória do planeta Marte registrada na figura? A ilustração destaca o movimento de Marte observado em intervalos de 10 dias, registrado da Terra: informação dada no enunciado da questão. A resposta para essa pergunta é a maior velocidade orbital da Terra faz com que, em certas épocas, ela ultrapasse Marte.
👉 Se prepare para o Enem e Vestibulares estudando Física de graça no Descomplica!
💚
A maior sala de aula direto da sua casa!
Junte-se aos 230 mil alunos que descobriram como melhorar os resultados estudando online! 👉 Clique aqui e saiba como!

