Matrizes e suas Operações: Guia Completo para estudar

Aprenda tudo sobre matrizes para que a sua prova de matemática não te pegue de surpresa!

Matriz é um assunto um tanto delicado, porém muito importante para o vestibular, já que questões sobre o assunto aparecem com grande frequência nas provas. Matriz e suas operações serão daqui pra frente um caso resolvido na sua vida!

Matriz

Matriz é uma maneira de guardar informações. Podemos organizar informações de diversas maneiras: listas, tabelas, espalhadas. Porém, com matrizes, pode-se realizar operações de muita utilidade com essas informações, tais como soma, produto, etc.

Como escrever uma matriz:

Exemplo de uma matriz com indicativos de linha e colunas, bem como seus elementos

Classificação

1. Matriz quadrada:
   Toda matriz que possui o mesmo número de linha e colunas.

Exemplo:

2. Matriz diagonal:
   É toda matriz que possui todos os elementos igual a zero, exceto na diagonal principal.

Exemplo de uma matriz diagonal, onde todos os elementos que não são da diagonal principal são iguais a zero.

3. Matriz transposta:
   Na matriz transposta, os elementos “trocam de posição”, e pode-se dizer que “linha vira coluna”, como mostrado no exemplo abaixo.

4. Matriz identidade:
   É uma matriz em que a diagonal principal tem todos os elementos igual a 1, e os demais elementos são zero.

Exemplo de matriz identidade. Ordem da matriz: nxn

5. Matriz inversa:
   É toda matriz que possui a seguinte propriedade: O produto entre a matriz original e a matriz inversa é igual a matriz identidade.

2 exemplos de matriz inversa, que é muito importante. Ambos de matrizes 2×2.

Soma de matrizes

Para somar matrizes, basta somar um a um cada elemento correspondente nas matrizes, assim como o exemplo abaixo.

Exemplo explicativo de soma de matrizes. Matrizes 3×2

Produto de matrizes

Produto de matrizes é uma operação muito importante e, certamente, a menos trivial dentre todas. Além disso, tem muita incidência nas provas, justamente por ser de grande importância.

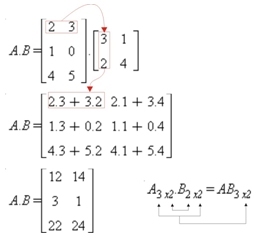Exemplo auto-explicativo de produto de matrizes. A é 3×2 e B é 2×2.

Exercícios

1. (FGV) Considere as matrizes

e seja C = AB. A soma dos elementos da 2a coluna de C vale:

a) 35
b) 40
c) 45
d) 50
e) 55

2. (PUCSP-03) Alfeu, Bento e Cíntia foram a uma certa loja e cada qual comprou camisas escolhidas entre três tipos, gastando nessa compra os totais de R$ 134,00, R$ 115,00 e R$ 48,00, respectivamente.

Sejam as matrizes

• os elementos de cada linha de A corresponde às quantidades dos três tipos de camisas compradas por Alfeu (1ª linha), Bento (2ª linha) e Cíntia (3ª linha);
• os elementos de cada coluna de A correspondem às quantidades de um mesmo tipo de camisa;
• os elementos de X correspondem aos preços unitários, em reais, de cada tipo de camisa;

Nessas condições, o total a ser pago pela compra de uma unidade de cada tipo de camisa é:

a) R$ 53,00
b) R$ 55,00
c) R$ 57,00
d) R$ 62,00
e) R$ 65,00

3. (MACK) Se A é uma matriz 3 x 4 e B uma matriz n x m, então:

a) existe A + B se, e somente se, n = 4 e m = 3;
b) existe AB se, e somente se, n = 4 e m = 3;
c) existem AB e BA se, e somente se, n = 4 e m = 3;
d) existem, iguais, A + B e B + A se, e somente se, A = B;
e) existem, iguais, AB e BA se, e somente se, A = B.

Gabarito

1. A

2. A

3. C