Sabemos, a partir do estudo de cinemática vetorial, que quando usamos vetores para definir posições e velocidades temos que tratar essas grandezas como grandezas vetoriais e usar dos artifícios matemáticos aprendidos para tais grandezas.
Agora, em Movimento Circular Uniforme, surge uma singularidade muito peculiar e com consequências bem definidas sobre a cinemática vetorial. Que tal aprender um pouco mais com o nosso resumo de hoje?
Definição de Movimento Circular Uniforme
Um corpo desempenha um movimento circular quando sua trajetória é uma circunferência ou um arco de circunferência. A palavra uniforme vem do fato de o corpo não mudar o valor da sua velocidade linear, ou seja, não dar voltas em tempos diferentes.
Existem milhares de exemplos de movimentos circulares, como o movimento dos corpos celestes, o movimento dos ponteiros do relógio, entre outros.

O movimento da Lua em relação à Terra pode ser reconhecido como um MCU.
Caraterísticas do Movimento Circular Uniforme
Você deve ter percebido na imagem anterior uma das características do MCU: sua aceleração é perpendicular à velocidade. Damos a essa aceleração o nome de centrípeta — que aponta para o centro —, e sua principal função é alterar a direção da velocidade, de modo a sempre manter o corpo em uma trajetória circular.
Nesse tipo de movimento, temos sempre duas maneiras de classificar as grandezas: lineares ou angulares.
Grandezas lineares
Todas as grandezas lineares atuam diretamente no corpo em questão. Exemplo: a velocidade v da imagem acima, a aceleração a e uma posição s que determina o tamanho do arco de circunferência percorrida pelo corpo.
Grandezas Angulares
As grandezas angulares são as que podem ser identificadas quando pensamos no centro da trajetória. Exemplo: imagine que no desenho anterior você estivesse girando a Terra junto com o corpo. Repare que a Terra teria uma velocidade em torno de seu próprio eixo. A essa rotação damos o nome de Velocidade Angular. O quanto a Terra giraria é definido por um ângulo.
Período e Frequência
Como sabemos, o Movimento Circular Uniforme tem velocidade linear sempre constante, uma consequência disso é que sempre é gasto o mesmo tempo para dar voltas completas sobre sua trajetória. A esse tempo damos o nome de período.
Todo movimento periódico é definido por ter um tempo para voltar a sua configuração inicial. O movimento circular uniforme é um movimento periódico e, portanto, tem também uma outra característica: a frequência.
Frequência é definida como o inverso do período e podemos concluir que ela é o quanto de “voltas” damos por “tempo”.
Frequência (f) é igual ao inverso do Período (T).
Unidades do SI
Para as medidas anteriormente estudadas, como velocidade e aceleração, mantêm-se as mesmas Unidades de Medidas Internacionais. Para as novas medidas, utilizam-se:
[f] = hertz
[T] = segundos
Velocidade Linear no MCU
Vamos considerar um carro fazendo uma trajetória circular, como no desenho abaixo:
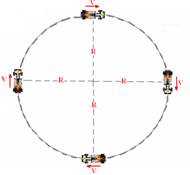
Imagem tirada do site www.fisicaevestibular.com.br
A velocidade linear do carro é constante, pois não há variação dela durante toda a trajetória circular. Sabendo que o tempo que o carro leva para completar uma volta completa é o Período (T) e o comprimento de uma circunferência pode ser dado por ![]() , podemos concluir que:
, podemos concluir que:
Velocidade Angular no MCU
A partir do desenho abaixo, e sempre tendo na mente que a velocidade é a variação de espaço dividido pela variação de tempo,
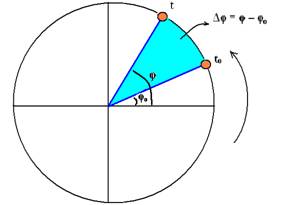
podemos concluir que:
Relação entre Grandezas Lineares e Angulares
Quando visualizamos da seguinte forma, podemos relacionar os movimentos lineares e angulares matematicamente.

Sabemos que o arco de circunferência acima se relaciona com o ângulo pela equação:
Podemos reparar que essa equação já é primordial para o entendimento da relação de medidas angulares com medidas lineares. Quando dividimos os dois lados por tempo, reparamos que:
Repare então que temos as relações de velocidades linear e angular:
Aceleração Centrípeta
Agora,vamos estudar o porquê de o movimento ter trajetória circular. Repare que, na primeira figura, temos em evidência a velocidade e também um vetor a. Esse vetor, chamado aceleração centrípeta, é o responsável pela mudança de direção da velocidade.
A aceleração centrípeta tem seu módulo calculado por:
Exercícios
1. (UEM) Sobre o movimento circular uniforme, assinale o que for correto.
01. Período é o intervalo de tempo que um móvel gasta para efetuar uma volta completa.
02. A frequência de rotação é dada pelo número de voltas que um móvel efetua por unidade de tempo.
04. A distância que um móvel em movimento circular uniforme percorre ao efetuar uma volta completa é diretamente proporcional ao raio de sua trajetória.
08. Quando um móvel efetua um movimento circular uniforme, sobre ele atua uma força centrípeta, a qual é responsável pela mudança na direção da velocidade do móvel.
16. O módulo da aceleração centrípeta é diretamente proporcional ao raio de sua trajetória.
Veja como resolver passo-a-passo esta questão!
2. (ENEM) Para serrar os ossos e carnes congeladas, um açougueiro utiliza uma serra de fita que possui três polias e um motor. O equipamento pode ser montado de duas formas diferentes, P e Q. Por questão de segurança, é necessário que a serra possua menor velocidade linear.
Por qual montagem o açougueiro deve optar e qual a justificativa desta opção?
a) Q, pois as polias 1 e 3 giram com velocidades lineares iguais em pontos periféricos e a que tiver maior raio terá menor frequência.
b) Q, pois as polias 1 e 3 giram com frequências iguais e a que tiver maior raio terá menor velocidade linear em um ponto periférico.
c) P, pois as polias 2 e 3 giram com frequências diferentes e a que tiver maior raio terá menor velocidade linear em um ponto periférico.
d) P, pois as polias 1 e 2 giram com diferentes velocidades lineares em pontos periféricos e a que tiver menor raio terá maior frequência.
e) Q, pois as polias 2 e 3 giram com diferentes velocidades lineares em pontos periféricos e a que tiver maior raio terá menor frequência.
Veja como resolver passo-a-passo esta questão!
3. (UFRGS) A figura apresenta esquematicamente o sistema de transmissão de uma bicicleta convencional.
Na bicicleta, a coroa A conecta-se à catraca B através da correia P. Por sua vez, B é ligada à roda traseira R, girando com ela quando o ciclista está pedalando.
Nesta situação, supondo que a bicicleta se move sem deslizar, as magnitudes das velocidades angulares, ωA, ωB e ωR, são tais que
a) ωA < ωB = ωR
b) ωA = ωB < ωR
c) ωA = ωB = ωR
d) ωA < ωB < ωR
e) ωA > ωB = ωR
Veja como resolver passo-a-passo esta questão!
Gabarito
1. 15
2. A
3. A







