Circunferência: 3 esportes que vão te fazer ver circunferências em todo lugar

O que os esportes tem a ver com matemática? Saiba tudo com esta lista sobre circunferência!

Com os jogos Pan-Americanos de Toronto, nada melhor do que enaltecer o quão maravilhoso pode ser um esporte na vida de uma pessoa. E como o esporte pode ajudar na sua vida de vestibulando? Além de aliviar um pouco dessa sua intensa vida de estudos, ele pode te fazer notar em alguns aspectos com outros olhos. Como? Você vai saber a partir de agora!

1) Motocross

O motocross é um esporte muito perigoso, principalmente quando se trata das acrobacias feitas pelos seus praticantes. Você já reparou que o looping feito por eles lembra muito uma circunferência? A maneira de saber como esta manobra se comporta é lembrando da Equação Geral ou da Equação Reduzida da Circunferência.
Lembrando que a Equação Reduzida é dada por:

Sendo que o ponto C (x₀, y₀) é o centro da circunferência e “r” é o raio dessa circunferência.
A partir dessa equação reduzida, resolvendo os produtos notáveis, podemos chegar na Equação Geral, que é dada por:

Em que C (x₀, y₀) é o centro da circunferência e “r” é o raio dessa circunferência, também.

Isso deve te deixar muito tonto…

2) Globo da Morte

Pode até ser que alguns não o considerem uma prática esportiva, mas o Globo da Morte é mais um esporte radical praticado com motos, em que o motociclista simplesmente deve ficar piruetando com seu veículo dentro de um globo, usando seus componentes de velocidade para vencer a ação da gravidade.
Quando essa moto se encontra no ponto mais alto dessa trajetória circular, ela fica praticamente sem contato com o globo, ou seja, fica tangente a essa trajetória, o que nos faz lembrar de uma reta tangente à circunferência:

A reta s é tangente à circunferência de centro O e raio r, isto é, a reta s possui um ponto em comum com a circunferência. Por isso, podemos dizer que a distância entre centro O e a reta s possui a mesma medida do raio dessa circunferência.

Isso é muito bizarro…

3) Arco e Flecha

Mudando agora para uma modalidade mais olímpica, quem nunca sentiu vontade de atirar uma vez uma flecha? Mas você já imaginou, por exemplo, se, numa flechada, acertarmos uma laranja de formato perfeitamente esférica? Essa flecha cortará uma secção circular, lembrando muito uma reta secante a essa circunferência.
Lembrando que uma reta secante a uma circunferência é uma reta que corta essa circunferência em 2 pontos:

Perceba que a reta s é secante à circunferência de raio r e centro O, e a reta intersecta a circunferência em dois pontos. Nesse caso, vimos que a medida do raio da circunferência é maior que a medida da distância entre o centro e a reta secante.
OBS: caso erremos a flechada nessa determinada laranja, podemos associar o erro ao fato de uma reta ser externa ou exterior a essa circunferência:

Nesse caso, a reta s é externa à circunferência de centro O e raio r. Podemos perceber que a distância do centro da circunferência à reta s é maior que o raio da circunferência.

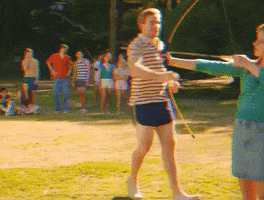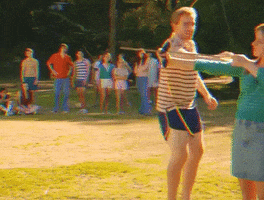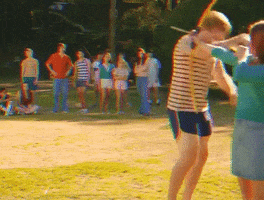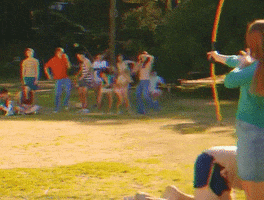
O cuidado nunca é demais…