Nós, que convivemos dia após dia nessa luta incessante que é o vestibular, sabemos que as questões, de todas as matérias, da matemática à redação, são contextualizadas, trazendo algum assunto abordado para o nosso dia-a-dia. Muitas vezes não sabíamos nem que aquele determinado assunto se aplicava assim no nosso cotidiano, não é verdade? Por isso, separamos 4 questões que te provam que a sua bicicleta pode te ajudar a ir bem no vestibular, sim! Basta olhá-la da maneira mais conveniente! =D

Depois de ler essa lista, você vai entender tão bem de bicicletas e cálculos como essa menininha.
1. GEOMETRIA PLANA (CIRCUNFERÊNCIA) E TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
Para responder essa questão, assista uma aula sobre Trigonometria.
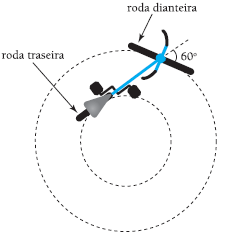
(UERJ – 2011) Um ciclista pedala uma bicicleta em trajetória circular de modo que as direções dos deslocamentos das rodas mantêm sempre um ângulo de 60º. O diâmetro da roda traseira dessa bicicleta é igual à metade do diâmetro de sua roda dianteira. O esquema a seguir mostra a bicicleta vista de cima em um dado instante do percurso.
Admita que, para uma volta completa da bicicleta, N1 é o número de voltas dadas pela roda traseira e N2 o número de voltas dadas pela roda dianteira em torno de seus respectivos eixos de rotação. A razão N1/N2 é igual a:
a) 1
b) 2
c) 3
d) 4
GABARITO:
A figura acima representa as trajetórias das rodas. O círculo menor é a trajetória da roda traseira e o maior da dianteira. O diâmetro da dianteira é o dobro do diâmetro da traseira, então:
D = 2d
onde D é diâmetro da dianteira e d, da traseira.
Portanto,
Rd = 2Rt
onde Rd é raio da dianteira e Rt da traseira.
Observando o triângulo PQT, vimos que sen(30º) = r/R,
½ = r/R
R = 2r
A distancia percorrida pela roda traseira é:
2π r
Assim, o número de voltas dadas por essa roda será:
2 π r/ 2 π Rt = r / Rt = N1
O mesmo acontece para a roda dianteira, perceba:
2π R
Assim, o número de voltas dadas por essa roda é:
2π R / 2π Rd = R/Rd = N2
Portanto, N1/N2 será:
(r / Rt ) / (R/Rd) = (r / Rt ) / (2r/2 Rt) = (r / Rt ) x (2 Rt /2 r) = 1.
Resposta: Letra A.

Esse é você, “bicicletando” na cara do vestibular.
2. ANÁLISE COMBINATÓRIA
Para responder essa questão, assista uma aula sobre Análise Combinatória.
(UERJ – 2008) Um dente da 1ª engrenagem da coroa quebrou. Para que a corrente não se desprenda com a bicicleta em movimento, admita que a engrenagem danificada só deva ser ligada à 1ª ou à 2ª engrenagem do pinhão. Nesse caso, o número máximo de marchas distintas, que podem ser utilizadas para movimentar a bicicleta, é de:
a) 10
b) 12
c) 14
d) 16
GABARITO:
Usando a engrenagem quebrada da coroa temos duas etapas (Engrenagem da coroa x Engrenagem do Pinhão), então:
1 x 2 = 2
Usando engrenagem que não esteja quebrada, temos:
2 x 6 = 12
Logo, temos 2 + 12 = 14 marchas distintas que podemos utilizar
Resposta: Letra C.
3. CIRCUNFERÊNCIA
Para resolver essa questão, assista uma aula sobre Circunferência.
(FGV) Abaixo está representado um sistema de transmissão, composto por duas polias e uma correia. As dimensões são mostradas na figura:

a) Determine o comprimento da correia. Dados: √33 = 5,74; √27 = 5,2
b) Sabendo que a polia menor faz 500 rotações por minuto e que traciona a polia maior, determine com quantas rotações por minuto a polia maior irá girar
GABARITO:
a) Perceba que o comprimento da correia é:
Co= t + 2x + y
No triângulo ABC, temos:
x² + 3² = 30² ó x² = 900 – 9 ó x² = 891 ó x² = 33 . 27 ó
ó X = √33 . √27 ó x = 5,75 . 5,2 ó x = 29, 848
O ângulo Beta será igual a:
2 x 84º = 168º
portanto, para calcular o arco que mede t, temos:
2πr = 2. π . 7 ——–> 360º
t ———–> 168º
t = 98 π/15
Quanto ao ângulo α, perceba que é 360º – 2 x 84 = 192º, logo, parar calcularmos o comprimento de arco y, usaremos o mesmo raciocínio:
2πr = 2. π . 10 ——-> 360º
Y ————–> 192º
Y = 32π/3
Portanto, o comprimento da correia será:
Co = 98 π/15 + 59,696 + 32π/3
Co = 59,696 + 86π/6
b) Queremos saber o número de rotações n da polia maior, em 1 minuto, portanto:
2π . 10 . n = 2π . 7 . 500
n = 350 rotações
4. TRIGONOMETRIA E RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
Para resolver essa questão, assista uma aula sobre Relações Métricas no Triângulo Retângulo.
(UNICAMP) Laura decidiu usar sua bicicleta nova para subir uma rampa. As figuras abaixo ilustram a rampa a ser vencida e a bicicleta de Laura.
a) Suponha que a rampa que Laura deve subir tenha ângulo de inclinação α, tal que cos(α) = √0,99. Suponha também que cada pedalada faça a bicicleta percorrer 3,15 m. Calcule a altura h que será atingida por Laura após 100 pedaladas
b) O quadro da bicicleta de Laura está destacado na figura. Com base nos dados dela, e sabendo que a mede 22cm, calcule o comprimento b da barra que liga o eixo da roda ao eixo dos pedais.
GABARITO:
a) Observando as figuras, vimos que a bicicleta terá que percorrer o comprimento da hipotenusa daquele triângulo retângulo. Se a cada pedalada , a bicicleta percorre 3,15 m, com as 100 pedaladas, ela percorrerá 315 m, que é o comprimento da rampa.
Sen(α) = h/315
H = 315 Sen(α)
(Sen(α))² + (cos(α))² = 1, e cos(α)= √0,99, temos:
Sen²(α) + 0,99 = 1
Sen²(α) = 0,01
Sen(α) = √0,01
Sen(α) = 0,1.
Assim,
h = 315 x 0,1 = 31,5 m.
b) No triângulo da direita no quadro da bicicleta são dados dois ângulos. Como a soma dos ângulos internos de qualquer polígono é dada por (n-2).180º, a soma dos ângulos internos do triângulo é 180º. Para descobrirmos o terceiro ângulo desse triângulo, fazemos 180 – 24 – 77 = 79º. Agora, podemos descobrir quanto vale o ângulo superior do triângulo da esquerda fazendo 180 – 79 – 26 = 75. Agora podemos calcular o terceiro ângulo desse triângulo fazendo 180 – 75 – 30 = 75º, logo, esse triângulo é isósceles. Assim, usando a lei dos cossenos, temos:
a² = b² + b² – 2.b.b.cos(30º) = 2b² – 2b². √3/2 = b² ( 2 – √3)
Logo, se a = 22, temos:
a² = b² ( 2 – √3)
b² = a²/( 2 – √3)
b = 22 / √( 2 – √3), que é a distância do eixo da roda até o eixo dos pedais.

Enfim, galera, agora vocês, naquele passeio de domingo, quando for andar de bicicleta com seus amigos, pais ou quem for, já podem prestar mais atenção na matemática envolvida em seu passeio, mas cuidado para não se distrair e esquecer que você está em duas rodas…