Física não precisa ser difícil! Confira aqui um resumo completo sobre Dilatação dos Sólidos e se prepare para gabaritar sua prova!
Uma maneira bem simples e direta de descrever o estudo da Dilatação é: parte da Física que estuda a variação no tamanho do corpo, sendo essa variação no tamanho causada por uma variação na temperatura do corpo.
Ou seja, o corpo terá sua temperatura modificada e, consequentemente, suas dimensões irão mudar.

Temperatura
Temperatura é o grau de agitação das moléculas. Quanto mais agitadas, maior a temperatura.
 Moléculas mais agitadas no corpo quente e menos agitadas no corpo frio
Moléculas mais agitadas no corpo quente e menos agitadas no corpo frioDilatação de Sólidos
Vimos que, conforme aumenta a temperatura, ocorre um aumento nas dimensões do corpo e que a temperatura é o grau de agitação das moléculas. Quanto maior é a agitação das moléculas, mais colisões existem entre elas, fazendo com que ocorra uma separação molecular maior.
A Dilatação dos Sólidos pode ser de 3 tipos:
Dilatação Linear
Quando apenas uma de suas dimensões é analisada. Geralmente é aplicado na dilatação de barras e cabos.
A variação no comprimento do sólido é dada pela expressão:

Onde Δl é a variação do comprimento da barra, α é o coeficiente de dilatação linear do material e ΔT é a variação da temperatura.
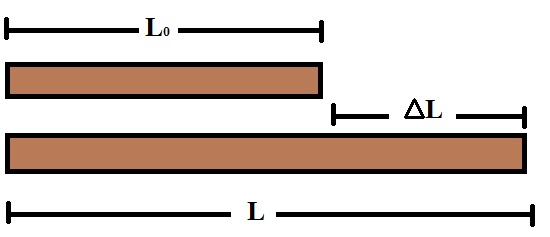 Variação em apenas uma dimensão é chamada de dilatação linear
Variação em apenas uma dimensão é chamada de dilatação linearSabendo que

Podemos utilizar a equação da seguinte forma também:

Dilatação superficial
Quando duas de suas dimensões são analisadas. Geralmente é aplicado na dilatação de placas ou chapas.
A variação na área do sólido é dada pela expressão:

Onde ΔA é a variação na área da placa, β é o coeficiente de dilatação superficial do material e ΔT é a variação da temperatura.
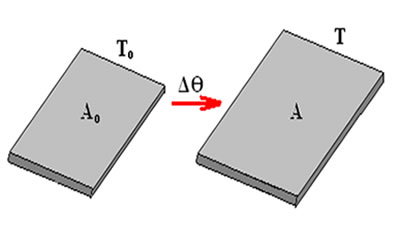 Variação em duas dimensões é chamada de dilatação superficial
Variação em duas dimensões é chamada de dilatação superficialSabendo que

Podemos utilizar a equação da seguinte forma também:

Dilatação volumétrica
Quando as três dimensões são analisadas. É aplicado a qualquer sólido em que as três dimensões tem comprimento variáveis.
A variação no volume do sólido é dada pela expressão:

Onde Δ V é a variação no volume do sólido, γ é o coeficiente de dilatação volumétrico do material e ΔT é a variação da temperatura.
 Variação em três dimensões é chamada de dilatação volumétrica
Variação em três dimensões é chamada de dilatação volumétricaSabendo que

Podemos utilizar a equação da seguinte forma também:

Coeficientes de Dilatação
A unidade padrão do SI para os coeficientes de dilatação é o grau Celsius recíproco (°C-1). Os três coeficientes de dilatação se relacionam da seguinte maneira:
β=2α e γ=3α
Uma dica: grave sempre que o α é o coeficiente de dilatação linear (uma dimensão) e que, conforme é acrescentado uma dimensão, acrescenta-se 1α no coeficiente de dilatação.
Lâminas Bimetálicas
São lâminas de materiais diferentes que estão unidas e sofrerão a mesma variação de temperatura. Como a variação na temperatura das lâminas é a mesma e o material é diferente (diferentes coeficientes de dilatação) um dos materiais da lâmina ira se dilatar mais do que o outro, curvando a lâmina.
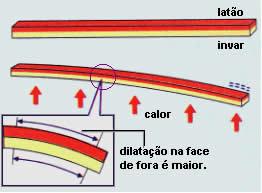 O metal com maior coeficiente de dilatação tem maior variação na dimensão
O metal com maior coeficiente de dilatação tem maior variação na dimensãoComo a variação na dimensão é diretamente proporcional ao coeficiente de dilatação, o material com maior coeficiente de dilatação terá a maior dilatação.
Exercícios
1. (UNESP-SP) A lâmina bimetálica da figura abaixo é feita de cobre (α= 1,4 x 10-5°C-1) e de alumínio (α = 2,4 x 10-5°C-1). Uma das partes não pode deslizar sobre a outra e o sistema está engastado numa parede.

Se na temperatura ambiente (27 °C) ela é horizontal, a afirmativa correta sobre o comportamento da lâmina (α é o coeficiente de dilatação linear) é:
a) Sempre se curva para baixo quando muda a temperatura.b) Sempre se curva para cima quando muda a temperatura.c) Curva-se para baixo se θ > 27 °C e para cima de θ < 27 °C.d) Curva-se para cima se θ > 27 °C e para baixo se θ < 27 °C.e) Somente se curva se θ > 27 °C.
2. (FGV-SP) Um serralheiro monta, com o mesmo tipo de vergalhão de ferro, a armação esquematizada.

A barra transversal que liga os pontos A e B não exerce forças sobre esses pontos. Se a temperatura da armação for aumentada, a barra transversal
a) continua não exercendo forças sobre os pontos A e B.b) empurrará os pontos A e B, pois ficará √2 vezes maior que o novo tamanho que deveria assumir.c) empurrará os pontos A e B, pois ficará (L0)αΔT vezes maior que o novo tamanho que deveria assumir.d) tracionará os pontos A e B, pois ficará √2 vezes menor que o novo tamanho que deveria assumir.e) tracionará os pontos A e B, pois ficará (L0)αΔT vezes menor que o novo tamanho que deveria assumir.
3. (UFRJ-RJ) Um quadrado foi montado com três hastes de alumínio (αAl = 24 x 10-6C-1) e uma haste de aço (αaço = 12 x 10-6 C-1), e todas inicialmente à mesma temperatura.

O sistema é, então, submetido a um processo de aquecimento, de forma que a variação de temperatura é a mesma em todas as hastes.Podemos afirmar que, ao final do processo de aquecimento, a figura formada pelas hastes estará mais próxima de um:
a) quadrado.b) retângulo.c) losango.d) trapézio retângulo.e) trapézio isósceles.
Gabarito
1. D
2. A
3. E

