Entenda um pouco mais sobre lógica e a sua importância na Matemática
Lógica é um estudo que une duas áreas consideradas opostas: a matemática e a filosofia.É matemática, pois esta é a ciência dos padrões e tem na lógica o seu maior pilar. É filosofia, pois nela estudamos, entre outras coisas, pensamento e construção de raciocínios. Muitas pessoas sentem dificuldade em questões de lógica por deixarem de estudar, pensando que todo mundo já nasce sabendo raciocínio lógico, mas não é bem assim.
Aliás, ter dificuldade no tema, o que é bem frequente, traz consequências em todas as disciplinas, não só na matemática e na filosofia. Por isso, escrevemos um texto com asprincipais dicas para você aprender um pouquinho mais sobre o raciocínio lógico e como ele funciona.
1) O que é a lógica?
A primeira pessoa a estudar lógica foi Aristóteles, filósofo grego do século IV A.C.. É claro que, antes dele, as pessoas já pensavam logicamente, mas foi Aristóteles quem resolveu sistematizar e organizar as bases da compreensão do raciocínio lógico.
Aristóteles não entendia a lógica como uma ciência em si, mas como uma maneira pela qual pensamos corretamente. Tá, mas como assim? Se você refletir sobre o seu próprio pensamento, verá que existe uma sequência, uma cadeia de afirmações e ideias que nos levam a conclusões mais precisas. Tal processo é chamado de raciocínio.

De maneira geral,no estudo da lógica, nos interessa saber se a conclusão de um raciocínio constitui realmente uma consequência dos dados conhecidos e utilizados ou das hipóteses levantadas. Ou, como dizemos contidamente, se o que pensamos e dizemos “ faz sentido” ou se “tem razão”.
👉 Se prepare para o Enem e Vestibulares estudando Matemática de graça no Descomplica!
2) Proposição:
Uma proposição é uma sentença, verdadeira ou falsa, que exprime um pensamento completo. E, olha, precisa ser completo mesmo, ok? Por exemplo:
→"x + 1 = 2"não é uma proposição, pois ela ainda está em aberto. Diversos valores são atribuídos a x, os quais podem tornar a sentença verdadeira ou falsa.
→"1 + 1 = 2"é uma proposição verdadeira.
→"3 + 1 = 2"é uma proposição falsa.
Tendo essa definição bem consolidada, podemos seguir para asbases da lógica matemática.Na verdade, há dois postulados fundamentais para o raciocínio lógico. Vale lembrar que postulados são fatos admitidos sem a necessidade de demonstração, ou seja, a gente aceita e segue o baile.
Princípio do terceiro excluído: uma proposição só pode ser verdadeira ou falsa. Não há um meio termo.
Princípio da não contradição: nenhuma proposição pode ser verdadeira ou falsa ao mesmo tempo.
Tais postulados podem parecer óbvios, mas aposto que você já errou isso alguma vez na vida. Então, não subestime.
3) Negação de uma proposição:
A negação de uma proposição é uma outra proposição com um sentido oposto ao da original. Assim, a negação da proposição “amanhã vou à praia” é a proposição “amanhã não vou à praia”. Reparem que apenas umas destas proposições é verdadeira #TeamFicareiEmCasa.
Matematicamente falando, dada uma proposição p, sua negação é representada por~p. São apenas símbolos, não se assustem. Dito isso, podemos montar a seguinte tabela, chamadatabela verdade:
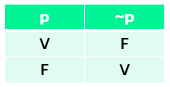
Conseguem ver que uma proposição e sua negação são necessariamente sentenças excludentes? Ou seja, se uma é verdade, a outra, com certeza é falsa.
4) Conectivos:
Sim, é isso mesmo que você leu. Existem conectivos em matemática, também. Eles funcionam de maneira muito similar àquela em português: elas conectam proposições. Ou seja, funcionam como conjunções.
Conectivo “e”:
O símbolo desse conectivo é^e sua utilização sugere a ideia de simultaneidade. A sentença resultante só será verdadeira se, e somente se, ambas as proposições forem verdadeiras. Por exemplo, dadas as proposições p e q:
→p: 1 + 1 = 2(Verdadeiro)
→q: 2 x 3 = 5(Falso)
→p ¨q: (1 + 1 = 2)e(2 x 3 = 5)é uma proposição falsa, pois a segunda parte é falsa.
Assim, podemos montar outra tabela verdade!
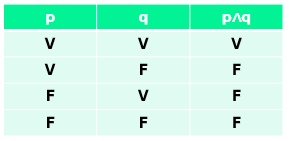
Como falamos antes, a sentençap ^qsó será verdade se p e q forem verdadeiras simultaneamente.
Conectivo “ou”:
O símbolo desse conectivo éve sua utilização sugere a ideia de união. A sentença resultante será verdadeira se e somente se, pelo menos, uma proposição for verdadeira. Por exemplo:
→p: 1 + 1 = 2(Verdadeiro)
→q: 2 x 3 = 5(Falso)
→p v q: (1 + 1 = 2)ou(2 x 3 = 5)é uma proposição verdadeira, pois a primeira parte é verdadeira.
Vamos à outra tabela verdade:
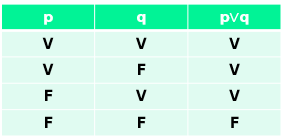
Veja que, nesse caso,p v qserá falsa apenas quando ambas as sentenças p e q forem falsas.
👉 Se prepare para o Enem e Vestibulares estudando Matemática de graça no Descomplica!
Condicional “se/então”:
Essa é uma das minhas preferidas! Usamos muito em matemática e é bem comum errarmos questões por causa dela. Seu símbolo é uma setinha bem simpática:⇒. Seu uso é viciante. Você começa a usar a seta e nunca mais quer escrever a palavra “então”.
Por exemplo:
Se eu acordar cedo, então irei à praia.
Acordo cedo⇒vou à praia.
Em nosso dia-a-dia,estamos razoavelmente acostumados a entender o sentido lógicode frases como essa. Ou seja, você entende que, se eu não for à praia, é porque não acordei cedo, concorda? E a ideia é essa mesmo! Uma proposição condicional “se p, então q” só será falsa se a proposição antecedente p for verdadeira e a consequente, falsa. Dá uma olhada na tabela verdade:
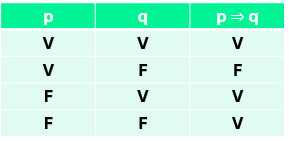
Bicondicional “se, e somente se”:
Fala sério, você já viu essa expressão sendo usada diversas vezes, não? Inclusive, já a usamos neste texto. Agora, você vai aprender de uma vez por todas como usá-la e quando ela é usada. Para isso, vamos voltar ao exemplo anterior:
Se eu acordar cedo, então irei à praia.
Nós até conversamos sobre entender que, se eu não fui à praia, então eu não acordei cedo. Mas, digamos que alguém tenha me visto na praia, isso quer dizer que eu, de fato, acordei cedo? Essa é a parte que pode confundir algumas pessoas.
A frase é bem clara: “se eu acordar cedo, então irei à praia”. Isso não quer dizer que, se eu for à praia, então, eu acordei cedo. A frase só me conta o que vai acontecer se eu acordar cedo. E se eu não acordar cedo? Não sei! Está em aberto. É aqui que entra a bicondicional, pois tudo muda se eu falar:
Vou à praia se, e somente se, eu acordar cedo
Nesse caso, não há dúvidas: se eu acordei tarde, não fui à praia. Conseguiu sentir a diferença?
O símbolo de uma bicondicional é uma setinha dupla⇔:
Vou à praia⇔acordo cedo
Uma proposição bicondicional p⇔q só será verdadeira se ambas p e q forem verdadeiras ou falsas:
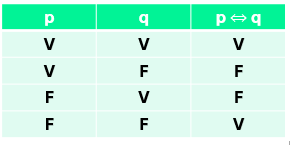
Pronto,acabamos de ver aquilo que é essencial para começar a entender lógica. Não é tão óbvio quanto parece, não é mesmo? Minha dica é ir lendo as tabelas verdade com atenção e atribuindo um sentido às proposições p e q. Você vai ver que funciona!
Para treinar, separei duas questões de vestibular para você. Dá só uma olhada:
1) Na cidade litorânea de Loretin é rigorosamente obedecida a seguinte ordem do prefeito:
“Se não chover, então todos os bares à beira- mar deverão ser abertos.”
Pode-se afirmar que:
a) Se todos os bares à beira-mar estão abertos, então choveu.
b) Se todos os bares à beira-mar estão abertos, então não choveu.
c) Se choveu, então todos os bares à beira-mar não estão abertos.
d) Se choveu, então todos os bares à beira-mar estão abertos.
e) Se um bar à beira-mar não está aberto, então choveu.
2) Cada um dos cartões abaixo tem um lado um número e do outro uma letra.
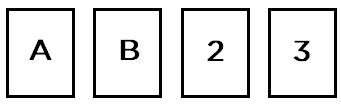
Alguém afirmou que todos os cartões que têm uma vogal numa face têm um número par na outra. Para verificar se essa informação é verdadeira:
a) é necessário virar todos os cartões
b) é suficiente virar os dois primeiros cartões.
c) é suficiente virar os dois últimos cartões.
d) é suficiente virar os dois cartões do meio
e) é suficiente virar o primeiro e o último cartão
f) é suficiente virar o primeiro e o terceiro cartão
Gabarito
1) Reparem que a frase dá instruções apenas para o caso em que não há chuva: todos os bares devem abrir. Por isso, nada pode ser dito sobre o caso em que há chuva, ou seja, os bares podem abrir, ou não, não sabemos, de fato. Sendo assim, eliminamos as alternativas A, C e D.
A letra B pode ser eliminada porque a proposição original não é uma bicondicional, ou seja, a primeira proposição (“Se não chover”) implica a segunda (“todos os bares estão abertos”), mas a segunda não implica a primeira. Como foi dito antes, nada pode ser dito sobre o caso em que há chuva, assim, não podemos afirmar a letra B.
Por fim, o gabarito é a letra E, pois, em uma condicional, ao negarmos a segunda proposição, negamos, também, a primeira. Ou seja, se existe algum bar que não esteja aberto, então quer dizer que choveu.
2) De novo, neste exercício, temos uma condicional. Lembre-se que, a condicional só nos diz o que acontece em um cenário. Nessa questão, sabemos o que acontece quando há uma vogal nesse cartão: o lado oposto é um número par. Assim, sabemos que, se um cartão tiver um número ímpar em uma de suas faces, então, a face oposta é, com certeza, uma consoante. Entretanto, não sabemos o que acontece quando um cartão possui uma consoante – seu verso pode ser par ou ímpar, nada sobre isso nos foi dito.
Assim, precisamos virar o primeiro cartão, para nos certificar que há um número par em seu verso e virar o último cartão, para verificar que não há uma vogal em seu verso. Tá, mas e o cartão de número 2? Nenhum problema, se ele possui uma consoante em seu verso, está tudo ok. Gabarito letra F.
👉 Se prepare para o Enem e Vestibulares estudando Matemática de graça no Descomplica!
💚
A maior sala de aula direto da sua casa!
Junte-se aos 230 mil alunos que descobriram como melhorar os resultados estudando online! 👉Clique aqui e saiba como!

