
Estude as principais características do movimento circular e que realmente importam para o vestibular.
Um movimento circular, na Mecânica Clássica, é aquele que um ponto material (ou o centro de massa de um corpo extenso) se desloca em uma trajetória circular. Uma força resultante centrípeta muda de direção o vetor velocidade, sendo continuamente aplicada para o centro da trajetória circular. Esta força é responsável pela chamada aceleração centrípeta, orientada para o centro da circunferência.
Pode haver ainda uma aceleração tangencial, que obviamente deve ser compensada por um incremento na intensidade da aceleração centrípeta a fim de que a trajectória não deixe de ser circular. O movimento circular é classificado, de acordo com a ausência ou a presença de aceleração tangencial, em movimento circular uniforme (MCU) e movimento circular uniformemente variado (MCUV). Trataremos apenas, porém, no MCU, haja visto que é o mais cobrado nos vestibulares tradicionais.
1. Propriedades do movimento circular
No movimento circular são introduzidas propriedades angulares como deslocamento angular, velocidade angular e aceleração angular e centrípeta. No caso do MCU, existe ainda o período
T, que é propriedade também utilizada no estudo dos movimentos periódicos.
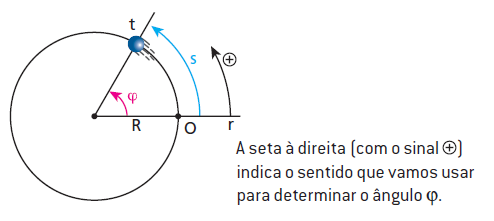
O deslocamento angular (indicado por θ ou φ [depende da fonte]) se define de modo similar ao deslocamento linear. Porém, ao invés de considerarmos um vetor deslocamento, consideramos um ângulo de deslocamento. Há um ângulo de referência, adotado de acordo com o problema.
Vejamos a relação entre as grandezas lineares e angulares:

onde R é o raio da trajetória circular.
Figura 01. Definição matemática do deslocamento angular.
2. Movimento circular uniforme
Como fica evidente pelas conversões, esses valores angulares não são mais do que maneiras de se expressar as propriedades lineares de forma conveniente ao movimento circular. Uma vez que a direção dos vetores deslocamento, velocidade e aceleração modifica-se a cada instante, é mais fácil trabalhar com ângulos. Tal não é o caso da aceleração centrípeta, que não encontra nenhum correspondente no movimento linear.
Surge a necessidade de uma força que produza essa aceleração centrípeta, força que é chamada analogamente de força resultante centrípeta, dirigida também ao centro da trajetória. A força centrípeta é aquela que mantém o ponto material em movimento circular, provocando a constante mudança da orientação do vetor velocidade.
A aceleração centrípeta pode ser expressa por:
acp=v²/R =²R
Figura 02. Relação vetorial entre a aceleração centrípeta e o vetor velocidade linear no MCU.
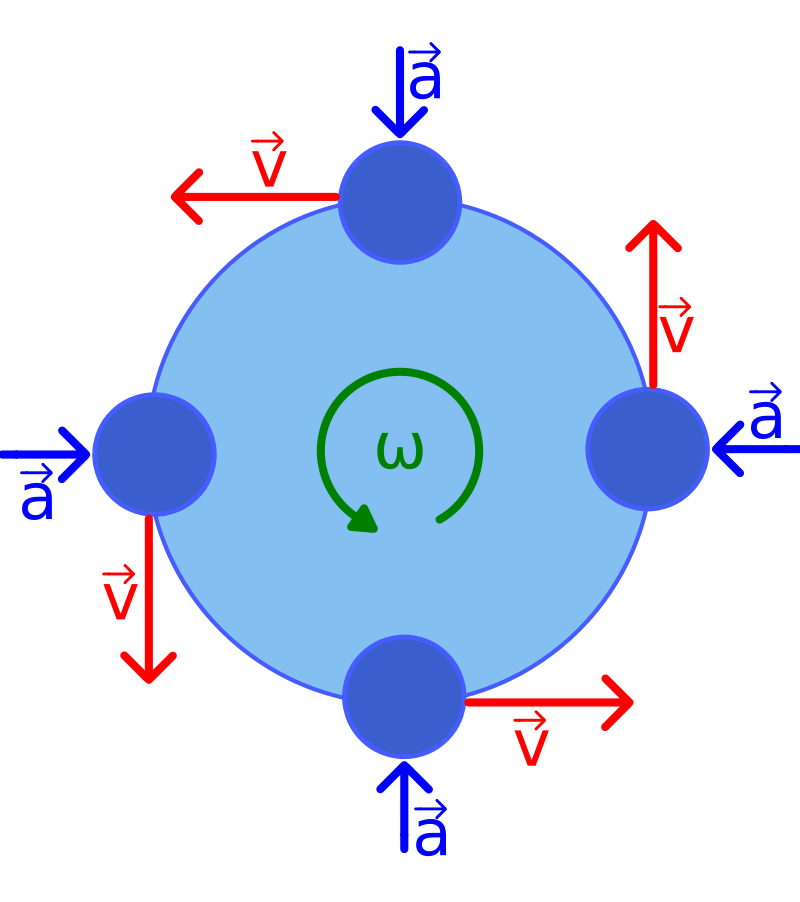
O MCU é um movimento periódico, isto é, todas as suas características se repetem em iguais intervalos de tempo. Cada intervalo corresponde ao tempo que a partícula leva para completar uma volta. Esse tempo denomina-se período do MCU e é simbolizado por T.
Período (T) de um MCU é o intervalo de tempo decorrido durante uma volta de uma dada partícula.
Outra grandeza referente ao MCU é a frequência, simbolizada por f. Suponha, por exemplo, que uma partícula complete uma volta em 0,1 s. Esse valor é o período (T) do movimento. Quantas voltas ela completa na unidade de tempo, no caso, 1 s? Efetuando o cálculo, percebemos que ela completa dez voltas por segundo. Dizemos, então, que essa é a sua frequência (f): f = 10 voltas/s
Assim, definimos:
A frequência (f) do movimento circular e uniforme executado por uma partícula é o número de voltas que essa partícula efetua por unidade de tempo. Assim, se a partícula efetua n voltas durante um intervalo de tempo ∆t, sua frequência é dada por:
f = n/∆t

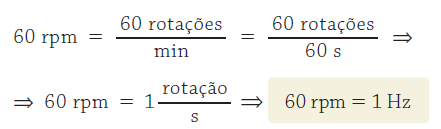
Na prática, é muito comum medir frequência em rotações por minuto (rpm). Para fazer conversões entre as unidades rpm e Hz, podemos usar a seguinte relação:
Relação entre frequência f e período T:
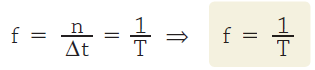
3. Transmissão de movimento circular
Acoplamento de polias e rodas dentadas
Polias podem ser acopladas por meio de correias ou por contato direto, de modo que uma polia rotando pode fazer a outra rotar também. Da mesma forma, rodas dentadas podem ser acopladas por contato direto ou por meio de correntes.
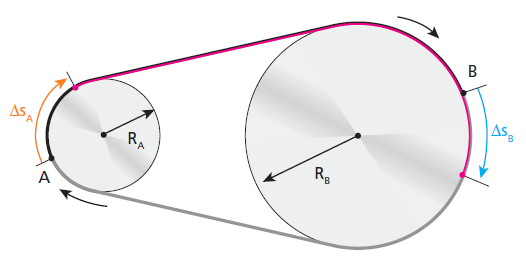
A figura 03 representa duas polias de raios RA e RB que rotam no mesmo sentido, acopladas por uma correia que não desliza sobre elas.
Aqui, os pontos A e B estão nas periferias das polias. Enquanto A se desloca SA, B se desloca SB. Como SA=SB, temos que:
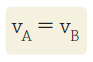
Figura 03. Acoplamento tangencial.
Fonte: Tópicos de Física - Vol.1 - Mecânica inclui Hidrodinâmica - 21ª Ed. 2012. Acessado em 28/02/2020.
Perceba, que temos:
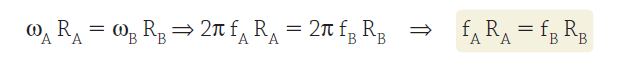
👉 Se prepare para o Enem e Vestibulares estudando Física de graça no Descomplica!
💚
A maior sala de aula direto da sua casa!
Junte-se aos 230 mil alunos que descobriram como melhorar os resultados estudando online! 👉 Clique aqui e saiba como!

