Quinta-feira é dia de Matemática! o/
Preparado para aprender tudo sobre Teorema de Tales e Semelhança? Os professores PC Sampaio e Alex Amaral estão mais do que preparados para te ensinar tudo o que você precisa saber desse assunto para mandar muito bem nos vestibulares e ENEM. 
Não esqueça de verificar, abaixo, os horários das aulas e baixe o material de apoio :D
Não esqueça de verificar, abaixo, os horários das aulas e baixe o material de apoio :D
Matemática: Teorema de Tales e SemelhançaTurma da Manhã: 10:15 às 11:15, com o professor PC Sampaio.
Turma da Noite: 19:45 às 20:45, com o professor Alex Amaral.
Faça download dos materiais, é só clicar aqui embaixo :)
MATERIAL DE AULA AO VIVO
1. O dono de um sítio pretende colocar uma haste de sustentação para melhor firmar dois postes de comprimentos iguais a 6m e 4m. A figura representa a situação real na qual os postes são descritos pelos segmentos AC e BD e a haste é representada pelo EF, todos perpendiculares ao solo, que é indicado pelo segmento de reta AB. Os segmentos AD e BC representam cabos de aço que serão instalados.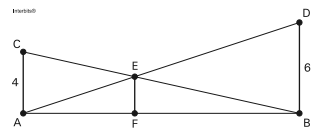
Qual deve ser o valor do comprimento da haste EF?
a) 1m
b) 2m
c) 2,4 m
d) 3m
e) 
Gabarito
1. C
LISTA DE EXERCÍCIOS
1. A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metro. A distância em metros que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é a) 1,16 metros. b) 3,0 metros. c) 5,4 metros. d) 5,6 metros. e) 7,04 metros. 2. Uma circunferência de raio 3 cm está inscrita no triângulo isósceles ABC, no qual
A altura relativa ao lado 
mede 8 cm. O comprimento de é, portanto, igual a
a) 24 cm
b) 13 cm
c) 12 cm
d) 9 cm
e) 7 cm
3. Considere a figura em que r // s // t .
O valor de x é
a) 3.
b) 4.
c) 5.
d) 6.
4. Numa festa junina, além da tradicional brincadeira de roubar bandeira no alto do pau de sebo, quem descobrisse a sua altura ganharia um prêmio. O ganhador do desafio fincou, paralelamente a esse mastro, um bastão de 1m. Medindo-se as sombras projetadas no chão pelo bastão e pelo pau, ele encontrou, respectivamente, 25 dm e 125 dm. Portanto, a altura do “pau de sebo”, em metros, é
a) 5,0.
b) 5,5.
c) 6,0.
d) 6,5.
Gabarito
1. D
2. C
3. B
4. A
PRINTS DA AULA
