Você sabia que você pode estudar pontos notáveis sem precisar levantar da sua cama? Confira e descubra o que matemática e os filmes no seu computador têm em comum!
Ah, como é bom ver filmes e seriados, não é? Deitar na sua cama confortável, pegar um pacote de biscoito, uma garrafa de água e uma barra de chocolate e curtir a madrugado vendo filmes… Mas você sabia que agora você pode fazer isso lembrando dos conceitos estudados aqui no Descomplica? Como? Vamos descobrir!
Acomode-se na sua cadeira e vamos estudar!
1) Aperte o Play
Para que possamos assistir aos nossos filmes e seriados favoritos, precisamos de um botãozinho, um cara que nem nos damos conta, mas que é muito importante, o botão de Play! Se você reparar, o botão do Play nos lembra muito um triângulo inscrito em uma circunferência, perceba:
E devemos lembrar que o centro da circunferência que circunscreve esse triângulo é o circuncentro. O circuncentro é o ponto de encontro das 3 mediatrizes de um triângulo.
A mediatriz de um triângulo é o segmento que forma 90° com o lado dividindo-o exatamente ao meio.
2) Assistindo Harry Potter
Muitos dizem que é uma das histórias mais bem boladas de bruxos e mundos encantados, mas o que ninguém diz é que com as relíquias da morte você pode visualizar um ponto notável de um triângulo! Se você reparar, o símbolo das relíquias da morte mostra uma circunferência inscrita em um triângulo! O centro dessa circunferência é o Incentro, que é o ponto de encontro das Bissetrizes do triângulo.
A Bissetriz de um um triângulo é o segmento que parte do vértice do mesmo e separa ao meio o ângulo referente a esse vértice.
O incentro é o centro da circunferência inscrita no triângulo
OBS: Lembre-se de que a Biessetriz é uma ceviana! Uma Ceviana é um segmento que parte de um vértice do triângulo e corta o lado oposto a ele.
Já podemos dar a desculpa de que estamos vendo Harry Potter para estudar quando nossas mães vierem perguntar!
3) Assistindo Velozes e Furiosos
Sem dúvidas um filme de muita ação e pouca física, certo? Mas é inegável o sucesso que essa série de filmes de luxuosos carros fez. Quando você vê aquelas marcas daqueles carrões, você não imagina que poderia visualizar um ponto notável ali, perceba:
Observe esse Logogotipo, ele passa a ideia de “Nooooossa, mas que carro!”
Você consegue visualizar um Baricentro nessa imagem? O baricentro é o ponto de encontro das 3 Medianas do triângulo, sendo uma mediana o segmento que parte de um vértice e corta o lado oposto exatamente na metade. Então, perceba:
O ponto vermelho do centro é o baricentro desse triângulo, pois cada “haste” prolongada cortaria exatamente na metade do lado oposto.
OBS: Não é porque o triângulo está inscrito em uma circunferência que todo ponto notável será o centro dela. Lembre-se: o Centro de uma circunferência circunscrita ao triângulo é formado pelo encontro das mediatrizes.
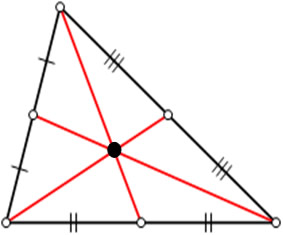O baricentro é formado pelo encontro de três cevianas chamadas medianas.
Então, galera, é isso, lembrem-se de que para entender os pontos notáveis basta você prestar muita atenção aos desenhos e saber quais são as principais cevianas de um triângulo.
