
No último resumo, iniciamos o estudo da Análise Combinatória e vimos quão próxima do dia a dia ela é e como é mais importante saber pensar do que ter um HD externo na cabeça.
QUER MANDAR BEM NOS ESTUDOS? A GENTE TE ENSINA O CAMINHO PRO SUCESSO!
Aliás, ao contrário do que grande parcela do mundo considera, a Matemática tem como um papel fundamental instigar a mente a pensar e desenvolver diversas áreas do cérebro, aperfeiçoando nossa visão espacial e psicológica do mundo, das pessoas e do meio em que vivemos.
Hoje, veremos Permutações e Combinações, aprofundaremos nosso conhecimento e aprimoraremos nossa percepção lógica.
Como a Análise Combinatória é dividida
Por ser um dos tópicos em que a matemática é dividida, a Análise Combinatória estuda os critérios para a representação da quantidade de possibilidades de um agrupamento sem a necessidade de desenvolvê-los.
Veja como a Análise Combinatória é dividida:
Permutações
Sendo M um conjunto com m elementos, isto é, M = {a1, a2, …, am}, chamamos de permutação dos m elementos a todo arranjo em que r = m. Portanto, Pm=m.(m-1).(m-2)…..[m-(m-1)].
Fatorial
Para simplificarmos as fórmulas de arranjos e permutações, além de outras que estudaremos futuramente, vamos definir o símbolo fatorial “!”.
Seja m um número natural maior ou igual a 2, definimos por m! o produto dos números consecutivos em ordem decrescente de m até 1, isto é: m! = m.(m-1).(m-2)…..3.2.1. Para m menor que 2, temos que 0! = 1 e 1! = 1.
Combinações
A Combinação está relacionada aos verbos escolher e selecionar, é um conjunto, logo a ordem não importa.
“Seja M um conjunto com m elementos, isto é, M = {a1, a2, a3, …, am}. Chamamos de combinações dos m elementos, tomados r a r, aos subconjuntos de M constituídos de r elementos.”
O número de combinações é dado por
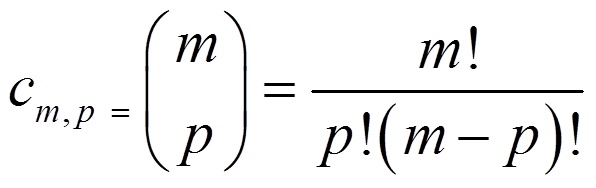
Permutações com elementos repetidos
A Permutação está relacionada aos verbos trocar e ordenar, é uma sequência, portanto a ordem importa e sequências iguais não devem ser contadas mais de uma vez, exemplo, a palavra Ana: ao permutarmos as duas letras “a”‘s, continuamos com anA, logo, consideramos que a sequência é a mesma.
Toda vez que tivermos números repetidos, devemos dividir a quantidade de permutações pelo fatorial da quantidade de elementos repetidos. Ou seja, sendo um conjunto de n elementos, dos quais n1 são iguais a a1, n2 são iguais a a2, …, nr são iguais a ar,
.
Fontes de Pesquisa:
Fundamentos da Matemática Elementar – Volume 5; Hazzan, Samuel.Sétima Edição – São Paulo: Atual, 2004.
EXERCÍCIOS
1. (ITA – SP) Quantos anagramas com 4 letras distintas podemos formar com as 10 primeiras letras do alfabeto e que contenham duas das letras a, b e c?
a) 1692.
b) 1572.
c) 1520.
d) 1512.
e) 1392.
2. (Unirio – RJ) Com os algarismos de 1 a 9, o total de números de 4 algarismos diferentes, formados por 2 algarismos pares e 2 ímpares, é igual a:
a) 126.
b) 504.
c) 720.
d) 1440.
e) 760.
GABARITO
1. D
2. D

