Conheça os 4 tipos de questões mais cobrados no ENEM sobre triângulos!
Fala, galera! As semanas passam e o nosso tão esperado ENEM fica cada vez mais perto! Neste espírito de revisões, preparamos um tema muito recorrente em provas: triângulos! Reunimos 4 questões das principais abordagens de triângulos que são cobrados no ENEM para que você possa se aproximar cada vez mais da nota 1000 em Matemática e suas Tecnologias!
DESCUBRA TUDO SOBRE TRIÂNGULOS E CONFIRA NOSSO GABARITO ENEM!
Agora você vai sambar na matemática
1) Condição de existência
Sabemos que, para que um triângulo exista, devemos respeitar algumas restrições:
a < b + c
b < a + c
c < a + b
Agora, temos a seguinte questão:
(ENEM 2014) Uma criança deseja criar triângulos utilizando palitos de fósforo de mesmo comprimento. Cada triângulo será construído com exatamente 17 palitos e pelo menos um dos lados do triângulo deve ter o comprimento de exatamente 6 palitos. A figura ilustra um triângulo construído com essas características.
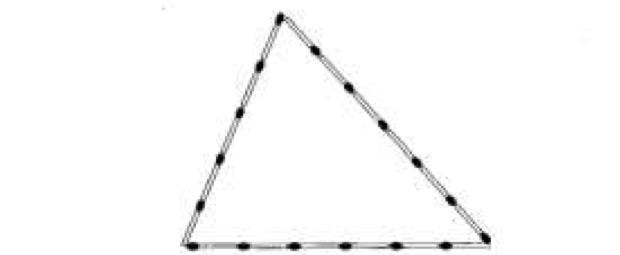
A quantidade máxima de triângulos não congruentes dois a dois que podem ser construídos é:
a) 3
b) 5
c) 6
d) 8
e) 10
RESOLUÇÃO:
Temos que o perímetro é 17 e que um lado é sempre A = 6. Assim, os possíveis valores para B e C são:
B = 1 e C = 10
B = 2 e C = 9
B = 3 e C = 8
B = 4 e C = 7
B = 5 e C = 6
Perceba que, a partir daí, os valores passariam a ser os mesmos, porém com letras trocadas. Agora, analisando quais valores satisfazem a condição de existência, temos:
10 < 1 + 6 -> Falso
9 < 2 + 6 -> Falso
8 < 3 + 6 -> Verdadeiro
7 < 4 + 6 -> Verdadeiro
6 < 5 + 6 -> Verdadeiro
Logo, como 3 pares de valores satisfazem a condição de existência, temos 3 diferentes triângulos que podem ser formados.
Gabarito: A
Você já sabe definições importantes!
2) Semelhança entre triângulos
Outro tópico muito importante dentro de triângulos são os casos de semelhança entre os triângulos. Lembre-se que dois triângulos são semelhantes quando seus lados são proporcionais e seus ângulos são congruentes. Agora, resolva a questão abaixo.
(ENEM 2013) O dono de um sítio pretende colocar uma haste de sustentação para melhor firmar dois postes de comprimentos iguais a 6m e 4m. A figura representa a situação real na qual os postes são descritos pelos segmentos AC e BD e a haste é representada pelo segmento EF, todos perpendiculares ao solo, que é indicado pelo segmento de reta AB. Os segmentos AD e BC representam cabos de aço que serão instalados.
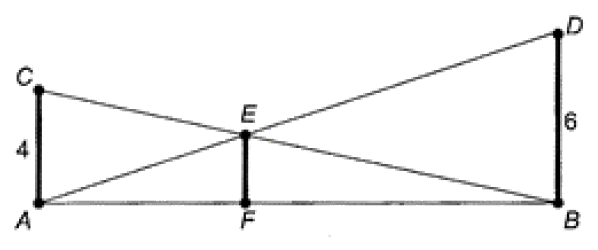
Qual deve ser o valor do comprimento da haste EF?
a) 1 m
b) 2 m
c) 2,4 m
d) 3 m
e) 2√6 m
RESOLUÇÃO:
Perceba, pela semelhança de AEF e ADB:
EF/6 = AF/AB
Pela semelhança de BEF e BCA, temos:
EF/4 = FB/AB
Agora, somando as igualdades, temos:
EF/ 6 + EF/4 = AF/AB + FB/AB
EF/ 6 + EF/4 = 1
4.EF + 6EF = 24
EF = 24/10
EF = 2,4 m,
Gabarito: C
3) Área do triângulo
As questões de áreas e volumes são muito recorrentes na prova do ENEM. Temos que a área de um triângulo é dada por:
Em que B é o comprimento da base e h é a altura desse triângulo.
Perceba como esse tema é cobrado na prova do ENEM com essa questão de 2012:
(ENEM 2012) Para decorar a fachada de um edifício, um arquiteto projetou a colocação de vitrais compostos de quadrados de lado medindo 1 m, conforme a figura a seguir.
Nesta figura, os pontos A, B, C e D são pontos médios dos lados do quadrado e os seguimentos AP e QC medem 1/4 da medida do lado do quadrado. Para confeccionar um vitral, são usados dois tipos de materiais: um para a parte sombreada da figura, que custa R$ 30,00 o m², e outro para a parte mais clara (regiões ABPDA e BCDQB), que custa R$ 50,00 o m². De acordo com esses dados, qual é o custo dos materiais usados na fabricação de um vitral?
A) R$ 22,50
B) R$ 35,00
C) R$ 40,00
D) R$ 42,50
E) R$ 45,00
RESOLUÇÃO:
Assim, temos que a região branca tem área de:
4 . (AP . MB/2) = 2. (1/4 . 1/2) = 1/4 m²
Logo, a área sombreada é de 3/4 m². Assim, a quantia que ele irá gastar será de:
30 . 3/4 + 50 . 1/4 = 35
Gabarito: B
Quando alguém tentar te perturbar nos estudos
4) Trigonometria no Triângulo Retângulo
Outro assunto que muitos morrem de medo de encarar é a trigonometria. Fique calmo! No ENEM, costuma-se cobrar uma trigonometria bem básica. Lembrando que, num triângulo retângulo, temos:
Agora, confira esta questão:
(ENEM 2011) Para determinar a distância de um barco até a praia, um navegante utilizou o seguinte procedimento: a partir de um ponto A, mediu o ângulo visual a fazendo mira em um ponto fixo P da praia. Mantendo o barco no mesmo sentido, ele seguiu até um ponto B de modo que fosse possível ver o mesmo ponto P da praia, no entanto sob um ângulo visual 2α . A figura ilustra essa situação:
Suponha que o navegante tenha medido o ângulo α=30o e, ao chegar ao ponto B, verificou que o barco havia percorrido a distância AB=2000m . Com base nesses dados e mantendo a mesma trajetória, a menor distância do barco até o ponto fixo P será:
RESOLUÇÃO:
A distância d é a menor distância entre o barco e o ponto P. Assim, temos:
cos 30 = d/2000
√3/2 = d/2000
d =1000√3
Gabarito: B
Você após resolver todas as questões
