Quer entender a fórmula da área do trapézio?
Uma das fórmulas mais diferentes de área é com certeza a do trapézio, então se você quer entender de onde veio a fórmula e arrasar nos exercícios, se liga neste post.
Vamos explicar tudo sobre a área do trapézio. Além disso, você vai ver os tipos de trapézios e uma aplicação sobre a área dessa figura geométrica. Vamos lá?
1. O trapézio
O trapézio é uma forma geométrica da família dos quadriláteros, logo ele possui 4 lados, sua característica é que ele possui dois lados paralelos, chamados de base maior (B) e base menor (b) e outros dois lados não paralelos. É traçado uma reta perpendicular referente ao vértice da base menor ao lado da base maior, chamado altura (h).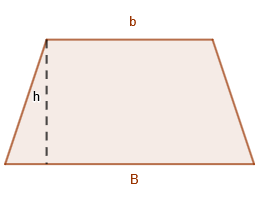
2. A fórmula do paralelogramo
Para entendermos a fórmula do Trapézio, precisamos relembrar a fórmula de um paralelogramo.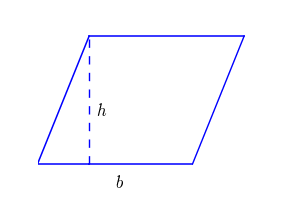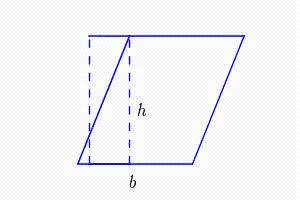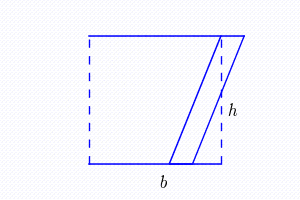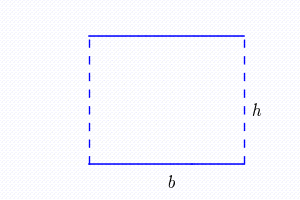
A fórmula do paralelogramo é base vezes a altura:
Ap= b.h
👉 Se prepare para o Enem e Vestibulares estudando Matemática de graça no Descomplica!
3. A fórmula do trapézio
Agora vamos associar o trapézio ao paralelogramo para entender sua fórmula, veja o trapézio abaixo: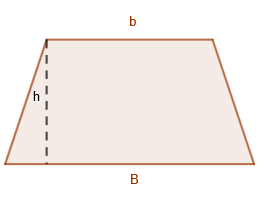
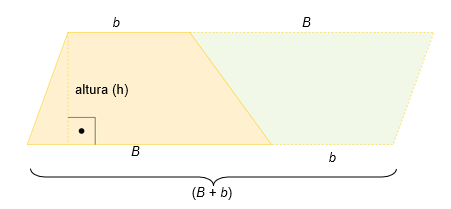
Observe que eu posso encaixar dois trapézios iguais sendo um virado pra baixo e o outro pra cima, da seguinte forma:
Temos que o desenho formado por esses dois trapézios é um paralelogramo, e como vimos a área do paralelogramo é dada por base vezes altura. Nesse caso a base é (B + b) e a altura é h. Que multiplicando temos:
Ap= b.h
Ap= (B + b).h
Como queremos saber a área de um trapézio, e no desenho temos dois, basta dividir a área encontrada por 2, temos:
AT=(B + b).h/2
Sendo essa a fórmula da área do Trapézio.
4. Tipos de trapézio
O trapézio possui 3 formas distintas que são: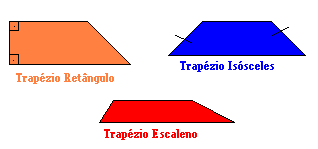
- O Trapézio retângulo é caracterizado por ter dois ângulos retos em seu interior.O Trapézio isósceles é caracterizado por ter dois lados (não paralelos) com mesma medida.
O Trapézio escaleno é caracterizada por ter todos os lados com medidas diferentes.
5. Aplicação em exercício
(UFCE) Seja PQRS um trapézio isósceles cujas bases menor e maior são respectivamente os segmentos PQ e SR. Se M e N são respectivamente as projeções ortogonais de P e Q sobre SR e a razão entre as medidas de SR e PQ é igual a três, então, pode-se afirmar corretamente que a razão entra a área do trapézio e a área do quadrilátero PQNM é igual a
a) 3,0
b) 1,5
c) 2,0
d) 2,5
Resolução: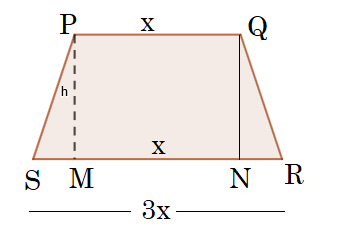
A área do trapézio é dada por:
AT=(B + b).h/2
AT=(3x + x).h/2
AT=4x.h/2AT= 2x.h
Já a área do quadrilátero é dada por:
Aq= b.hAq= x.h
Fazendo a razão entre as áreas, temos:
AT
/Aq=2xh/xh= 2
Resposta: Alternativa C.
6. Dicas de vídeos sobre Trapézio
Se você quer ver uma aula completinha sobre o tema e mais exercícios resolvidos, não perca essa aula da Titia Luanna: (exclusivo para alunos Descomplica).
Agora se você não é nosso aluno ainda, veja esse vídeo abaixo sobre áreas
👉 Se prepare para o Enem e Vestibulares estudando Matemática de graça no Descomplica!
💚
A maior sala de aula direto da sua casa!
Junte-se aos 230 mil alunos que descobriram como melhorar os resultados estudando online! 👉Clique aqui e saiba como!
