A coroa do Rei Hierão
Apresentação do Empuxo
Exemplos Básicos
Exercício de Empuxocom tração prendendo o corpo
Exercício de Empuxo com dinamômetro
Exercício de corpo flutuando em equilíbrio em um líquido
1. Princípio de Arquimedes
Consideremos um corpo sólido cilíndrico circular, de área da base A e altura h, totalmente imerso num fluido em equilíbrio, cuja densidade é d (Figura 1). Por simetria, vemos que as forças sobre a superfície lateral do cilindro se equilibram duas a duas [pressões (p, p) e (p´,p´) na figura]. Entretanto, a pressão p_2p2 exercida pelo fluido sobre a base inferior é maior do que a pressão p_1p1 sobre a base superior. Pelo teorema de Stevin:
p_2-p_1=dghp2−p1=dgh
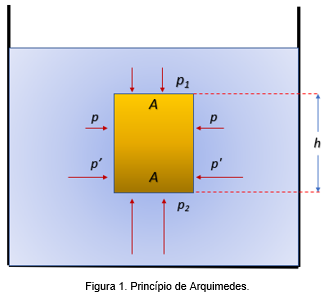
Logo, a resultante das forças superficiais exercidas pelo fluido sobre o cilindro será uma força vertical E ⃗, dirigida para cima, com:
E=p_2A-p_1A=dghA=dVg=mgE=p2A−p1A=dghA=dVg=mg
onde V = h.aV=h.a é o volume do cilindro e m = d.Vm=d.V é a massa de fluido deslocada pelo cilindro. Por conseguinte, o módulo da força E, que se chama empuxo, é dada por:
E=dVgE=dVg
Obs.: - dd é a densidade do fluido (d_{fluido}dfluido);
-VV é o volume do corpo que está submerso no fluido;
-gg é a intensidade do campo gravitacional local.
Com essas observações feitas, vamos reescrever o módulo do empuxo para não esquecermos desses detalhes importantes!
E=d_{fluido}.V{submerso}.gE=dfluido.Vsubmerso.g
Obs.: Perceba caro leito, que o empuxo é igual ao peso do volume do fluido deslocado!
2. Uma verificação da lei do empuxo
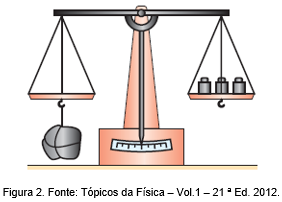
Consideremos a situação representada na Figura 2, em que se tem uma balança de travessão de braços iguais em equilíbrio. Nessas condições, o peso pendente na extremidade esquerda do travessão tem intensidade igual à do peso pendente na extremidade direita.
Admitamos, agora, a situação representada na Figura 3. Introduzindo o corpo de ferro não poroso (dependurado no prato esquerdo) em um recipiente contendo água, verificamos certo desequilíbrio da balança. Isso ocorre porque, ao ser imerso na água, o corpo de ferro recebe desta uma força vertical e dirigida para cima – o empuxo –, que provoca uma redução na intensidade da força que traciona a extremidade esquerda do travessão.

Na situação mostrada na Figura 4, o travessão encontra- se novamente em equilíbrio, tendo retornado à sua posição inicial. Para isso, foi necessário reduzir a intensidade do peso pendente à direita, retirando-se um dos massores do prato.
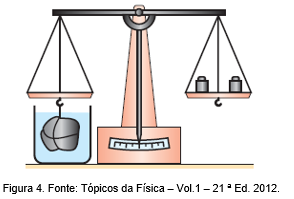
Supondo que a retirada de um massor do prato à direita tenha sido suficiente para recolocar o travessão na horizontal, podemos afirmar que a intensidade do peso desse objeto é igual à do empuxo recebido pelo corpo de ferro imerso na água.

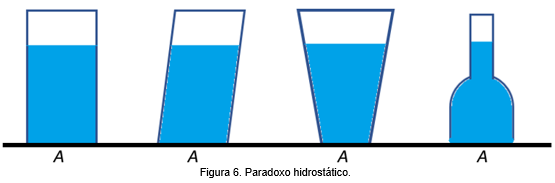
3. Paradoxo hidrostático:
Conforme já havia sido observado por Stevin e por Pascal, se tivermos recipientes de formas muito diferentes, como os da Figura 6, mas de mesma área da base AA, e se a altura hh do líquido é a mesma em todos, a força exercida sobre a base também é, embora o peso do líquido seja muito diferente (paradoxo hidrostático). Isto resulta da igualdade das pressões exercidas sobre o fundo, que só dependem da altura hh.
Entretanto, se equilibrarmos uma balança com um frasco vazio sobre o prato, e depois despejarmos líquido, a diferença de peso necessária para reequilibrá-la é igual ao peso do líquido. Para compatibilizar esses resultados, notemos que a força exercida pelo líquido sobre o prato da balança é a resultante de todas as forças exercidas pelo líquido sobre as paredes do frasco (Figura 7).
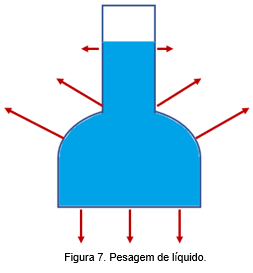
Estas forças, normais às paredes em cada ponto, são iguais e contrárias às forças pelas paredes sobre o líquido. Mas a resultante das forças superficiais sobre o líquido, como vimos na demonstração do princípio de Arquimedes, é igual e contrária ao peso do líquido. Logo, a resultante das pressões exercidas pelo líquido sobre as paredes, aplicadas ao prato da balança, é efetivamente igual ao peso do líquido.
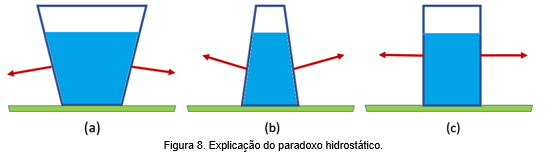
A explicação do paradoxo hidrostático resulta imediatamente dessas considerações. Assim, no caso da Figura 8 (a), a resultante das pressões sobre as superfícies laterais tem uma componente para baixo, que é responsável pela diferença entre o peso do líquido e a força sobre a base; no caso da Figura 8 (b), essa componente é para cima, e é somente no caso da Figura 8 © que a força sobre a base é igual ao peso do líquido.