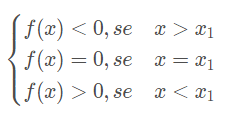Funções em Offline

Função Afim

Chama-se de função afim, ou função polinomial do 1°grau, toda função f de R em R dada pela lei de formação:

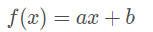
Em que a e b são números reais, tal que a ≠ 0, chamados de coeficientes numéricos, sendo a chamado de coeficiente angular e b, de coeficiente linear.

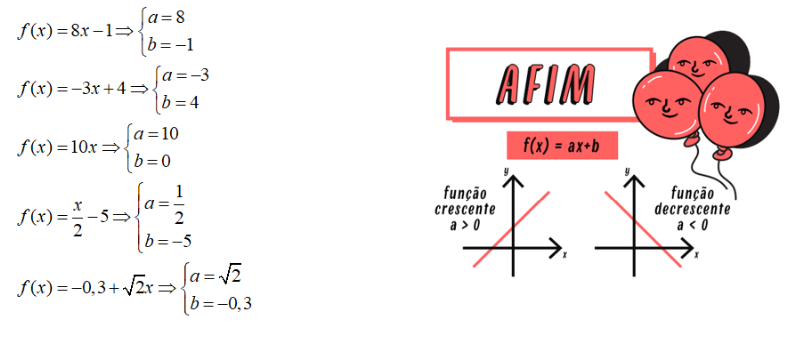
Exemplo: Na função definida por f(x) = x + 2, obtemos a = 1 e b = 2. Vejamos outros exemplos:

Função Linear

Há um caso particular de função afim que é definido quando b = 0. Assim, a função afim f de R em R, definida pela lei f(x) = ax, a ∈ R , é chamada de função linear. Dos exemplos tratados anteriormente, é linear a função dada por:

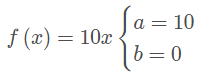
Taxa de Variação

Uma das características de uma função afim está relacionada à sua taxa de variação, que é constante; vejamos como identificar essa taxa de variação e como ela se relaciona com os valores das variáveis x e y, bem como com seus coeficientes numéricos.

Para entendermos melhor, vejamos um exemplo:

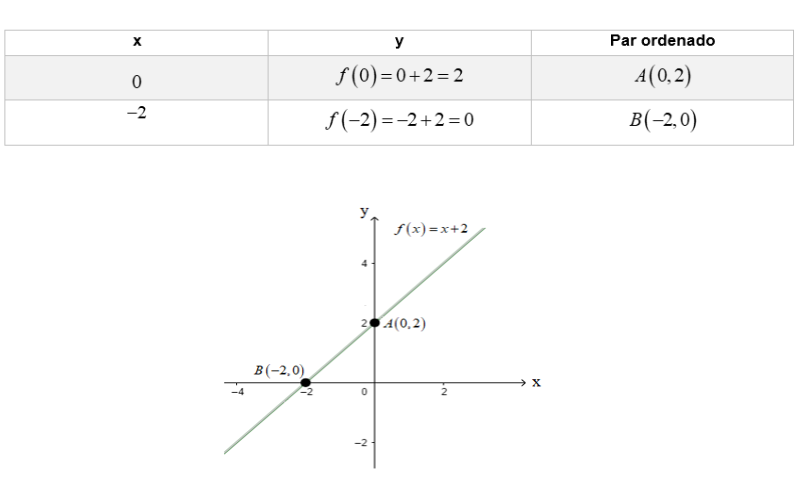
“Uma empresa, ao calcular seus custos, separa-os em custos fixos e custos variáveis. Os custos como aluguel, encargos fiscais, impostos e salários são considerados fixos, enquanto custos com matéria-prima, comissões pagas aos funcionários e custos com fretes são exemplos de custos variáveis. Vamos supor que uma empresa que produz certo material tem custo fixo de R$ 5.000,00 mensais e um custo variável, que depende do número de peças produzidas, de R$30,00 por unidade fabricada. Como podemos representar o custo mensal dessa empresa?”

Reparem que o custo inicial é de R$500,00, uma que, caso nenhuma unidade seja produzida, ainda assim esse seria o gasto da empresa. Além disso, a cada unidade fabricada, temos um aumento de R$30,00 no gasto total. Assim, podemos escrever a função do custo mensal da empresa em função do número de quantidades produzidas:

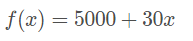
Em que f(x) é o gasto da empresa e xx é a quantidade de unidades produzidas.

Assim, propomos a seguinte pergunta: “O que acontece com o custo mensal da produção quando a quantidade de peças produzidas aumenta?”

Para responder a ela, vamos construir uma tabela de valores em que os valores de x aumentam uma unidade a cada linha.

Observando os valores de y, podemos concluir que, quando os valores da variável x sofrem um aumento de 1 unidade, os valores de y aumentam 30 unidades. Assim, podemos dizer que os valores de y sofrem um aumento constante a uma taxa de 30 unidades para cada unidade que aumentamos em x. Comparando o valor da taxa constante de aumento com os valores dos coeficientes a e b, concluímos que o valor da taxa de aumento é dado pelo valor do coeficiente numérico a, ou seja, o valor de a representa a taxa de variação da função afim f(x) = 5000 + 30x.

Agora que já sabemos a importância do coeficiente a, podemos aprender a calculá-lo. Dessa maneira, temos que a taxa de variação de uma função afim é dada pela razão entre a variação das ordenadas e a variação das abscissas de dois pontos quaisquer pertencentes à função. Logo, concluímos que a variação da função afim é dada por

a = ​Δx/​​Δy​​

Em que dado dois pontos, A(xa,ya) e B(x​b​​,y​b​​), obtemos Δx = x​a ​​− x​b​​ e Δy = y​a ​​− y​b​​

É importante saber:

• Se a > 0, temos uma função afim crescente.
• Se a < 0, temos uma função afim decrescente.

Representação Gráfica

Agora que já estudamos algumas propriedades e relações entre as variáveis x e y da função afim, devemos estabelecer qual é o comportamento dessa função em um plano cartesiano. Quando colocamos os pontos de uma função em um mesmo plano, determinamos uma curva que é chamada de gráfico da função. Para uma função afim f(x) = ax + b, com a ≠ 0 , o gráfico é uma reta oblíqua aos eixos 0x e 0y, ou seja, uma reta não paralela a nenhum dos eixos coordenados. Dessa maneira, para que possamos desenhar a reta que representa uma função afim, precisamos de apenas dois de seus pontos. Observe o exemplo abaixo:

Exemplo: Desenhar o gráfico de f(x) = x + 2

Vimos que precisamos de apenas dois pontos pertencentes à função f(x) = x + 2. Como podemos escolher quais pontos usar, é conveniente escolhermos os pontos de fácil cálculo, como os da tabela abaixo:

Agora, podemos, através dos pontos A e B, desenhar o gráfico da função f(x) = x + 2:

Aprenderemos abaixo algumas maneiras de facilitar a representação gráfica de uma função afim.

Coeficiente angular no gráfico

Dada uma função afim f(x) = ax + b, com a ≠ 0, seu coeficiente angular é dado por a = ​Δx/​​Δy​​. Graficamente, tomando dois pontos quaisquer de uma função afim, obtemos:

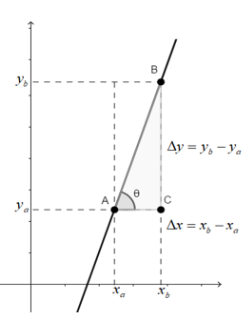
Note que, no triângulo retângulo ABC, temos os catetos AC ​​​= Δx = x​b​​ − x​a​​ e ​BC​​​ = Δy = y​b ​​− y​a​​.

Pela relação de tangente, temos:

tanθ =​​ AC​​​​​​/BC​​​​​ = ​Δx​​/Δy​​ = a

Ou seja, o coeficiente angular aa de uma função afim também pode ser expresso como a tangente do ângulo que a função faz com o eixo no sentido anti-horário.

Coeficiente linear no gráfico

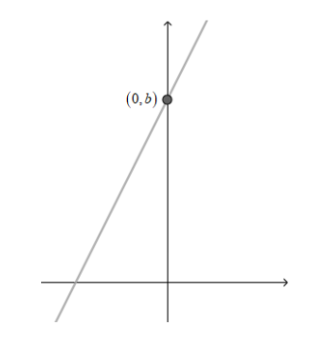
Seja uma função afim f(x) = ax + b, com a ≠ 0. Chamamos o coeficiente numérico b de coeficiente linear. O coeficiente linear é o valor de y encontrado quando x = 0.

Calculamos f(0):

f(0) = a*0 + b = b

f(0) = b

Assim, o coeficiente linear é a ordenada do ponto (0,b). No plano cartesiano, esse ponto representa a intersecção da reta com o eixo das ordenadas, ou seja, do eixo 0y.

Raiz ou zero da função

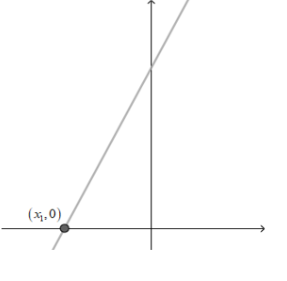
Por fim, devemos saber reconhecer um elemento importante do gráfico de uma função afim, que é chamado de raiz ou zero da função.

Em uma função afim f(x) = ax + b, a raiz é o valor de x quando y = 0. Isto é, para obter a raiz da função devemos igualar a zero o polinômio do 1° grau.

x​1​​ é raiz da função afim se, e somente se, f(x​1​​) = 0.

Na forma de um par ordenado, a raiz da função é a abscissa do ponto (x_1, 0)(x​1​​,0) que pertence ao eixo 0x0x do plano cartesiano.

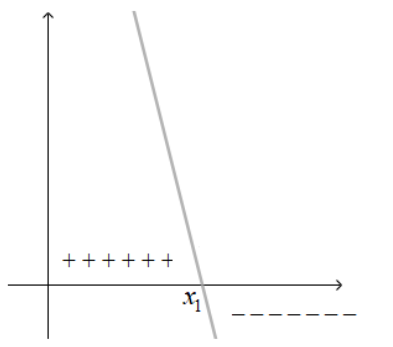
Estudo do sinal de uma função afim

Assim como para as equações, no estudo das inequações devemos, primeiramente, definir uma inequação para que, em seguida, possamos trabalhar com um tipo de inequação chamada de inequação do 1º grau.

Para analisarmos o sinal de uma função afim, precisamos separar em dois casos:

• Se a > 0, sendo x​1​​ a raiz da função, temos:
  
  

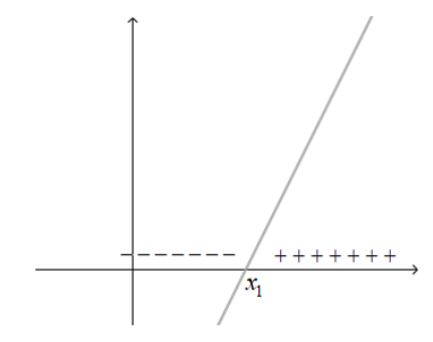
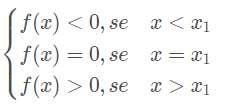
• Se a < 0, sendo x​1​​ a raiz da função, temos: