O que é um vetor?
Multiplicação por escalar
Aplicação na física
Adição de vetores
Exemplo de adição de vetores
Subtração de vetores
Na Física, temos como objetivo explicar a natureza e, para isso, fazendo diversas medições. Essas medidas podem ser grandezas escalares ou vetoriais. Vetores são grandezas que apresentam: Modulo, Direção e Sentido. Vamos entender isso melhor...
- Módulo: Representa a intensidade daquele vetor, podemos pensar nele como o número atrelado aquele vetor. Normalmente, representamos o modulo do vetor através do “tamanho” desse vetor. Assim se você encontrar um vetor grandão, é porque esse vetor tem um modulo grande.
- Direção: Representa o eixo onde esse vetor está posicionado. Inicialmente, vamos separar em duas direções: Horizontal e Vertical. Mais para frente vamos analisar vetores em diagonal e, também, vetores em direções perpendiculares (para situações em 3D). Mas calma... tudo ao seu tempo.
- Sentido: Representa o sentido para onde esse vetor aponta. Pense que dizer que um vetor está na horizontal não é o bastante, precisamos dizer se ele está apontando para esquerda ou para direita, por exemplo.
Dica: Pense que na representação vetorial (o desenho do vetor), a direção e a “traço” e o sentido e a “seta”. Isso pode ajudar a lembrar.
O objetivo dessa aula está em entender o que é um vetor e como fazer operações com esses vetores.
Operações Vetoriais
Multiplicação de um escalar por um vetor
Supondo o vetor abaixo:
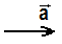
Esse vetor apresenta as seguintes características:
- Direção: Horizontal
- Sentido: Para direita
- Módulo ou intensidade: a = 1 unidade de medida (u.m.)
(para simplificar vamos escrever o módulo do vetor apenas como a.)
Dado um vetor b, vetor esse que apresenta um modulo igual a 3 vezes o modulo do vetor a. Calculando o módulo do vetor b, podemos dizer que b = 3a. Logo:
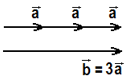
Pode-se concluir que o resultado do módulo de b vale 3 unidades.
Obs: É importante notar que quando se multiplica um vetor por um número escalar, sua direção e sentido não são alterados, porém caso o escalar seja negativo, a direção do vetor permanece a mesma, mas seu sentido será invertido.
Adição de vetores
Mesma direção e sentido
Quando efetuamos uma soma de dois vetores que apresentam a mesma direção e sentido, basta fazer a soma algébrica dos vetores.
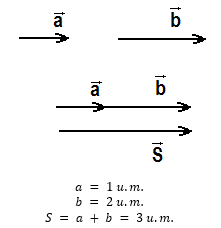
Mesma direção e sentidos opostos
Quando efetuamos uma soma de dois vetores que apresentam mesma direção, mas sentidos opostos, a soma se torna uma subtração.
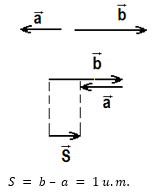
Obs: Embora a conta seja uma conta de subtração o desenho é o vetor soma. Isto acontece porque a soma vetorial não representa uma soma escalar comum. Note também que adotamos sinais para representar sentidos. O vetor b ganhou um sinal + e o vetor a ganhou um sinal -.
Direções Perpendiculares
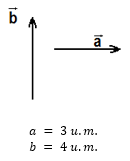
O vetor soma é dado pela junção dos vetores, sempre colocando a ponta do primeiro vetor junto do final do 2° vetor como na figura abaixo:
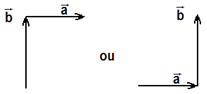
O vetor soma (S) será representado graficamente como uma seta que liga o início do 1° vetor ao final do 2° vetor. Assim:
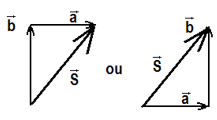
Esse método recebe o nome de regra do polígono, mas também podemos utilizar uma outra regra equivalente: A regra do paralelogramo. A regra do paralelogramo consiste em traçar retas paralelas aos vetores. Assim:
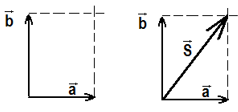
Para calcular o valor do vetor S (seu módulo) é preciso usar o Teorema de Pitágoras:
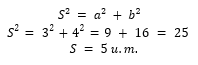
Direções quaisquer
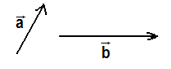
Aplicando a regra dos paralelogramos, podemos efetuar a soma vetorial dos vetores acima.
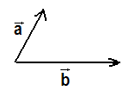
São traçadas retas paralelas aos vetores;
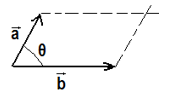
O vetor S será o vetor que tem como origem o encontro das origens dos demais vetores e como fim o encontro das retas paralelas aos vetores.
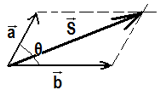
Desta forma é possível calcular o módulo de S utilizando a fórmula a seguir:
S¹ = a² + b² + 2.a.b.cosθ
Obs: Decomposição Vetorial. Fazer a decomposição é projetar o vetor em suas componentes ortogonais (eixo x e y).
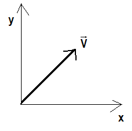
Considere um vetor v0 formando um ângulo α em relação a uma direção qualquer. Este vetor pode ser sempre decomposto em duas direções perpendiculares, sendo:
- v0x componente de v0 na direção x
- v0y componente de v0 na direção y
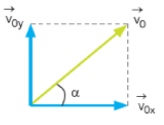
Os módulos destas duas componentes serão dados por:
- v0x = v0.cosθ
- v0y = v0.senθ
Substração de vetores
A operação de subtração de vetores pode ser feita pelas mesmas regras da adição.
Regra do Paralelogramo
1.º Faça linhas paralelas a cada um dos vetores, formando um paralelogramo.
2.º De seguida, faça o vetor resultante, que é o vetor que se encontra na diagonal desse paralelogramo.
3.º Faça a subtração, considerando que A é o vetor oposto de -B.
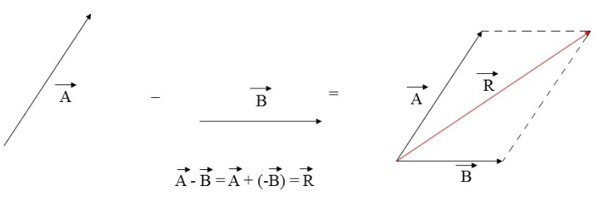
Regra do Poligonal
1.º Junte os vetores, um pela origem, outro pela extremidade (ponta). Faça assim sucessivamente, conforme o número de vetores que precisa somar.
2.º Faça uma linha perpendicular entre a origem do 1.º vetor e a extremidade do último vetor.
3.º Faça a subtração da linha perpendicular, considerando que A é o vetor oposto de -B.