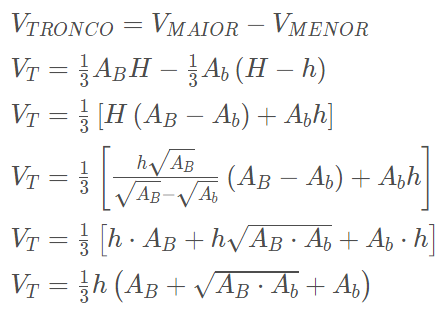Tronco e semelhança em Matemática

Relações de semelhança entre sólidos

Podemos estabelecer uma razão de semelhança entre as áreas e os volumes de dois sólidos semelhantes.
Observe os exemplos abaixo:
Sejam dois sólidos semelhantes, um pequeno e um grande,

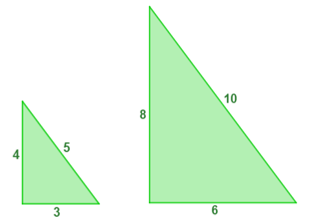
A razão das alturas desses sólidos é dada por:

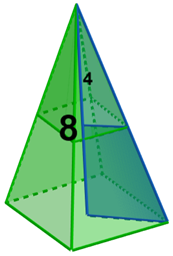
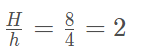
A razão das áreas desses sólidos é dada por:

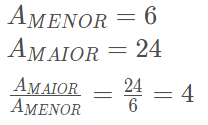
A razão entre os volumes desses sólidos é dada por:

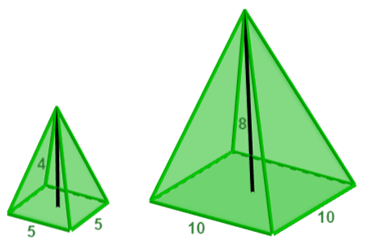
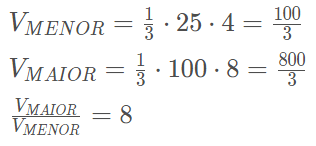
Podemos observar então, que dada a razão de semelhança da altura de dois solidos podemos obter também a razão da área e do volume desses sólidos. Observe:

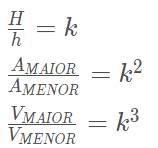
Tronco de uma pirâmide

Dado o tronco de uma pirâmide, podemos calcular o volume desse tronco subtraindo o volume da pirâmide menor do volume da pirâmide maior, observe:

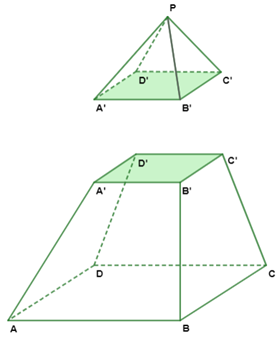
Sejam respectivamente, A_B​​ e HH a área da base e a altura da pirâmide maior e A_b​​ e h a área da base e a altura da pirâmide menor, temos que:

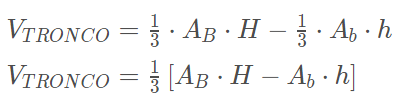
Tronco de um cone

Dado o tronco de um cone, podemos calcular o volume desse tronco subtraindo o volume do cone menor do volume do cone maior, observe:

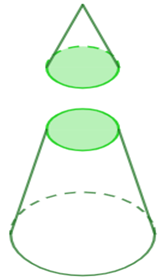
Sejam respectivamente, A​_B​​ e H a área da base e a altura do cone maior e Ab​​ e h a área da base e a altura do cone menor, temos que:

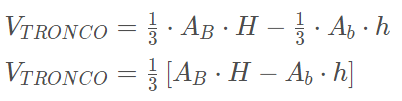
Tronco de um cilindro

Dado o tronco de um cilindro, podemos calcular o volume desse tronco subtraindo o volume do cilindro menor do volume do cilindro maior, observe:

Sejam respectivamente, AB​​​​ e H a área da base e a altura do cilindro maior e Ab​​ ​​ e h a área da base e a altura do cilindro menor, temos que:

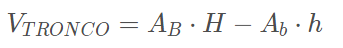
Demonstração da fórmula do tronco da pirâmide