Sequências em Matemática

Sequências: lei de formação, lei de recorrência e sequência Fibonacci

Lei de Formação

Em muitas situações da vida nos deparamos com sequências, sejam numéricas, imagéticas, de sons, de cores… O que há em comum em todas são os padrões, pois cada sequência apresenta um padrão, uma lei de formação.

Exemplo:

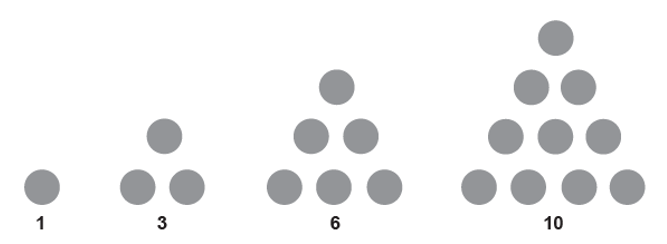
Nesta sequência observamos que aumentamos uma bolinha no lado do triângulo a partir da segunda posição. A listagem de quantidades não é uma sequência em si, 1, 3, 6, 10, mas podemos observar que há uma sequência na quantidade que se aumenta as bolinhas: da primeira imagem para a segunda aumentamos 2 bolinhas, da segunda para a terceira imagem aumentamos 3 bolinhas e da terceira para a quarta imagem aumentamos 4 bolinhas, logo, 2, 3, 4,... Assim, a partir disto, podemos saber quantas bolinhas terá a próxima imagem (que ocuparia a quinta imagem), pois aumentaria 5 bolinhas da anterior, logo, teríamos 15 bolinhas.
Algumas sequências são dadas por regras ou leis matemáticas chamadas leis de formação, que possibilitam explicitar todos os seus termos.
Por exemplo, dada a sequência (1, 4, 9, 16, 25) observamos que:
                                                                                     1=1²
                                                                                     4=2²
                                                                                     9=3²
                                                                                    16=4²
                                                                                    25=5²
Logo, a lei de formação é n².

Definimos:
a₁ = primeiro termo da sequência, a₂ = segundo termo da sequência, e assim sucessivamente, até generalizarmos para, a_n = enésimo termo da sequência.

Lei de recorrência

É uma regra que permite calcular qualquer termo de uma sequência utilizando termos anteriores.

Exemplo 1:

A sequência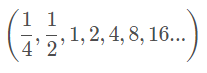  

Pode ser definida recursivamente por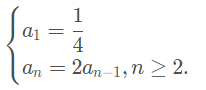 

Sequência de Fibonacci

A sequência de Fibonacci foi estudada no século XII pelo matemático italiano Leonardo Fibonacci (1170-c. 1250). Ela é infinita e sua lei de formação é baseada em um processo recursivo, ou seja, seus termos são calculados com base nos termos anteriores. Desse modo, para podermos construí-la, é necessário definirmos os dois primeiros termos, de modo que a₁ = 1, a₂ = 1 e, para n≥3, os termos são calculados a partir da soma dos dois termos anteriores:

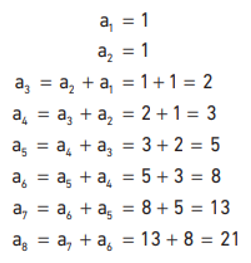
Assim, podemos concluir que a sequência de Fibonacci é dada por: (1, 1, 2, 3, 5, 8, 13, 21...).