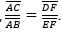Retas paralelas cortadas por uma transversal
Exercício de aplicação
Teorema de Tales
Aplicação do Teorema de Tales
Ângulos complementares, suplementares e replementares
Retas paralelas cortadas por uma transversal
Sejam r e s duas retas paralelas e uma reta t, concorrente a r e s:

A reta t é denominada transversal às retas r e s. Sua intersecção com as retas determina oito ângulos. Com relação aos ângulos formados, podemos classificá-los como:
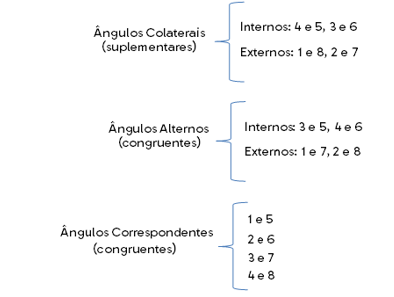
Com isso, podemos demonstrar como a soma dos ângulos internos de um triângulo vale 180°.
Seja ABC um triângulo. Trace a reta que passa por BC em seguida, tome a reta paralela a BC passando por A, conforme a figura abaixo:
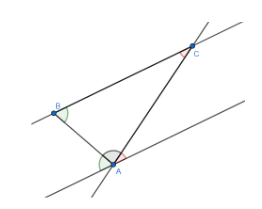
Note que a reta que passa por A e por C é transversal às duas outras retas. Com isso o ângulo ACB (ângulo vermelho) e ABC (ângulo verde) tem seus alternos internos na reta que passa por A. Podemos reparar também que a soma do ângulo verde com o ângulo vermelho e o ângulo cinza dá 180°, conforme queríamos provar.
Teorema de Tales

Se um feixe de retas paralelas e cortado por duas retas transversais, os segmentos determinados sobre a primeira transversal são proporcionais a seus correspondentes determinados sobre a segunda transversal.
Por Tales:
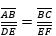
Usando as propriedades de proporção, podemos reescrever a proporção acima de outras formas ainda mais completas, como, por exemplo,