A resultante
Conceito de resultante
Método da linha poligonal
Aplicação da linha poligonal
Método da decomposição
Conceito e tipo de força
Quando pensamos em “força” logo fazemos uma associação com a ideia de força mecânica, como por exemplo, no caso da força que fazemos para empurrar, levantar, atirar, puxar ou apenas segurar algo.
A força é uma grandeza vetorial, possuindo módulo, direção e sentido. Sua unidade no Sistema Internacional é o newton (símbolo: N) em homenagem ao cientista inglês Isaac Newton.
Aparecerão dois tipos de forças durante o estudo da Física, são elas:
- Força de campo: são aquelas que atuam à distância, sem a necessidade de contato entre os corpos. Ex.: força gravitacional (peso) e força magnética;
- Força de contato: são aquelas em que existe a necessidade de um contato físico entre os corpos para que neles atuem a força. Ex.: força normal, força de atrito, tração e força elástica.
Operações com vetores
Soma vetorial
Pode ser feita de 2 formas, pela regra do polígono ou pela regra do paralelogramo. As duas formas irão dar o mesmo resultado, porém, em alguns casos, fazer uma das regras será mais fácil do que a outra.
Como escrever uma soma vetorial:
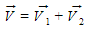
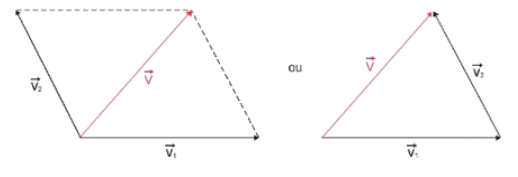
Na imagem abaixo temos a regra do paralelogramo à esquerda e a regra do polígono à direita.
Veja que os vetores somados são os mesmos, ou seja, tem mesmo módulo, direção e sentido.
- Regra do paralelogramo: os vetores são unidos pela origem e traçadas retas paralelas, formando o parelelogramo. Depois é só traçar um vetor que saia da mesma origem dos vetores somados e ligar ao vértice do paralelogramo que não tinha vetor encostando.
- Regra de polígono: os vetores são unidos de uma forma diferente. A origem de um vetor sempre será colocada na extremidade do outro vetor. Após todos os vetores serem colocados seguindo esse padrão, traçasse um vetor que saia da origem do primeiro vetor até a extremidade do último vetor.
Multiplicação por um escalar:
Seja V o vetor a ser multiplicado pelo número real n, resultando no vetor U
Ou seja,
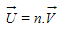
Este vetor U terá as seguintes características:
- Módulo: U = n.V
- Direção: a mesma de V se n ≠ 0
- Sentido: o mesmo de V se n > 0 e oposto V se n < 0
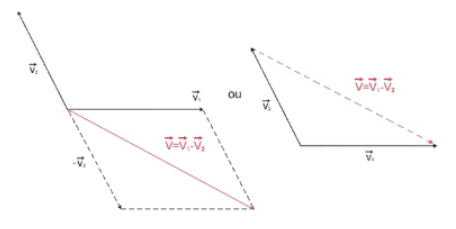
Diferença vetorial
Considere a seguinte diferença de vetores:
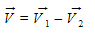
Para resolver esta situação, iremos inverter o sentido do vetor 2, ou seja, pegaremos o seu oposto e iremos somar com o vetor 1:
Cinemática Vetorial
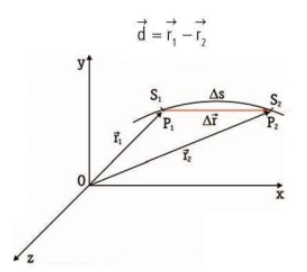
Vetor deslocamento d
Vetor que une o ponto de partida (𝑆0) ao ponto de chegada (𝑆)
É importante notar que a posição de qualquer ponto é descrita por um vetor que vai do referencial até o determinado ponto. Ou seja, o vetor deslocamento será a diferença dos vetores posição inicial e posição final.
Distância percorrida ≠ Deslocamento
Imagine a seguinte situação: Leonardo irá viajar do Rio de Janeiro para Manaus e pretende ir de carro. O vetor deslocamento é feito traçando uma reta que vai do Rio de Janeiro até Manaus. O módulo desse vetor deslocamento é dado pelo tamanho do vetor.
A distância percorrida pelo Léo Gomes será medida pelo odômetro (aquele dispositivo do carro que mede a quilometragem).
Ou seja, para o vetor deslocamento só é importante o ponto de partida e o ponto de chegada, não importando a trajetória. Mas você concorda que se o Léo Gomes for do Rio de Janeiro direto para Manaus é diferente do que ele também ir do Rio de Janeiro para Manaus passando antes pelo Chile? Nessas duas situações, o vetor deslocamento será o mesmo, mas a distância percorrida será, nitidamente, diferente.
Velocidade vetorial instantânea V
A velocidade vetorial V da partícula, num instante t, terá as seguintes características:
- Módulo: igual ao módulo da velocidade escalar V no instante t
- Direção: da reta tangente à trajetória da partícula
- Sentido: o mesmo do movimento