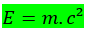Relatividade Restrita em Física

Os postulados de Einstein

Ate então, a Física se ateve a determinadas bases que conhecemos hoje em dia como Bases da Mecânica Clássica. Essas bases foram formadas por Isaac Newton em sua obra Princípios Matemáticos da Filosofia Natural. Com o passar dos anos, vimos que essa base funcionava para o mundo que nossos olhos enxergavam e se limitava a isso. Na construção da Newton, temos algumas grandezas que são tidas como grandezas absolutas:

• Tempo
• Comprimento
• Massa

Quando adotamos essas grandezas a situações onde temos corpos próximos da velocidade da luz, percebemos que esse conceito de grandeza absoluta não funciona. Ou seja, essas grandezas se tornam grandezas relativísticas.

A teoria da relatividade foi desenvolvida por Albert Einstein entre 1905 e 1915. Essa teoria é dividida em duas situações:

Relatividade Restrita: Onde temos situações envolvendo referencias inercias
Relatividade Geral: Onde temos situações envolvendo referenciais não inerciais

Nesse material, vamos focar na Relatividade Restrita, já que ela é um estudo possível com o nível matemático que temos no Ensino Médio.

Para a teoria da relatividade, Einstein desenvolveu dois postulados que ficaram conhecidos como Postulados de Einstein. Sendo eles:

• As leis da física são as mesmas, expressas por equações que tem a mesma forma, em qualquer referencial inercial
• A velocidade da luz no vácuo tem o mesmo valor “c” em relação a qualquer referencial inercial, tal que: c ≅ 3 . 10⁸​ m/s

A dilatação do tempo

A dilatação do tempo diz respeito comportamento do tempo quando observamos corpos que se deslocam próximos da velocidade da luz. Para isso, é proposta a seguinte situação:

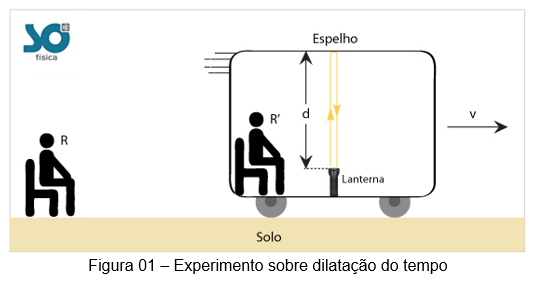
É colocado dois observadores R (fora de um trem) e R’ (dentro de um trem) para observar um feixe de luz vindo de uma fonte posicionada no chão do trem. Esse feixe tem movimentação vertical e para cima, onde encontra um espelho no teto. Após sofrer reflexão, esse feixe retorna. O objetivo desse experimento é entender o comportamento da luz quando comparamos as observações de um referencial R’ com o de R. Esse experimento mostra que o intervalo de tempo para cada um dos observadores não é o mesmo, entrando em conflito com a ideia de tempo absoluto para qualquer referencial.

Para o referencial R’, encontramos um valor clássico para o intervalo de tempo, já que esse observador está em movimento com a fonte:

∆t’ = 2d / c

Sendo “c” a velocidade da luz no vácuo e d a distância entre o chão e o teto do vagão do trem. Como a luz sobe e desce, temos “2d”. Agora, para o referencial R, o movimento é diferente

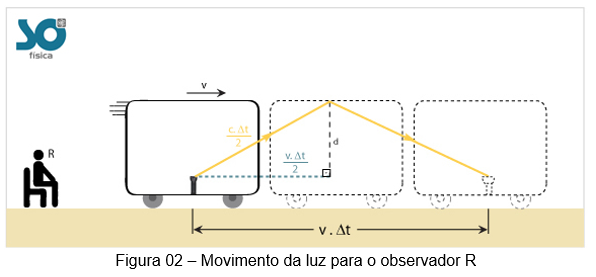
Para esse observador, temos um intervalo ∆t de valor diferente. Comprando com o intervalo de tempo do observador R’, temos:

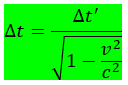
A contração do comprimento

Nosso objetivo agora é analisar como objetos próximos da velocidade da luz consegue medir comprimentos. Vamos lembrar do nosso experimento com os observadores R e R’. Temos um observador R que está fora de um trem observando o trem entrar em um túnel. Para R, o túnel tem um tamanho natural que vamos chamar de L. Mas será que para R’, que está próximo da velocidade da luz, o túnel tem o mesmo comprimento?

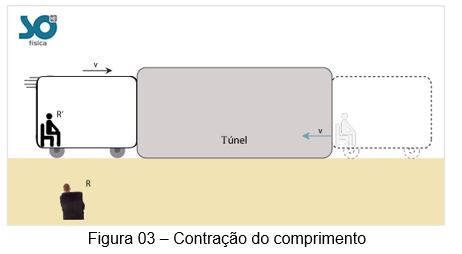
A resposta é não! Para o observador R’, o túnel vai ter um comprimento menor que para o observador R. Podemos calcular essa compressão do comprimento da seguinte forma:

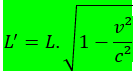
Massa relativística

Antes de começarmos, vamos fazer uma determinação a respeito do conceito de massa. Normalmente, determinamos o conceito de massa como a quantidade de matéria que um determinado corpo apresenta. Esse é o conceito que a Química apresenta nos seus estudos, por exemplo. Para a Física, principalmente agora, vamos adotar um novo conceito. A massa será definida como o grau de dificuldade que um corpo possui ao ser submetido a uma determinada aceleração. A partir disso, podemos observar como a massa de um corpo pode sofrer modificações quando submetido a altas velocidades.

Para determinado corpo submetido a altas velocidades, podemos observar que a massa sofre alterações a partir dessa expressão:

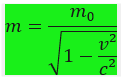
Sendo “m” a massa do corpo sendo medido por um observador em altas velocidades e “m_0m​0​​” a massa do corpo sendo medida por um observador inercial.

Equivalência massa e energia

Nosso objetivo aqui é fazer uma relação entre massa e energia, relação essa feita por Einstein. Sabe quando você estuda na química uma reação exotérmica? Essa reação não libera energia do nada! Você estudou que energia não é criada e nem destruída, então, se temos liberação de energia, essa energia tem que ter vindo de algum lugar!

Essa energia vem de uma pequena porção de massa que é transformada em energia. Isso acontece em reações instáveis que nos conhecemos bem na história do nosso planeta… um tal de bomba atômica.

Em uma fusão nuclear, onde temos uma reação com átomos de hidrogênio, temos a seguinte reação:

H + H → He + energia

No Sol, temos em torno de 4 milhões de toneladas de massa por segundo se tornando energia. Essa energia é a energia que nosso planeta recebe em forma de radiação.

Essa relação entre energia e massa tem a seguinte forma:

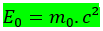
Sendo “E₀​​” a energia de repouso de um corpo. “m₀” a massa de repouso do corpo e “c” velocidade da luz no vácuo.

Vamos ver um exemplo: Imagine que temos um corpo de massa m₀​​ = 1 g. Quanto teríamos de energia se esse corpo fosse transformado puramente em energia? c ≅ 3.10⁸​​ m/s

E₀ = 0,01 . 3 . (10⁸)²
E₀ = 9 . 10³ J

Lembre-se que a massa deve ser passado para Quilograma (kg) para encontrar a energia em Joule (J)
Agora, a expressão acima esta ligada a massa e energia de repouso, ou seja, quando meu objeto está parado. Mas e se meu objeto estiver em movimento? Sabemos que a massa dele é diferente em movimento de acordo com a equação da massa relativística. Então, a energia de um corpo em movimento com altas velocidades é:

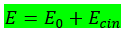
Sendo:

E₀ = m₀ . c²

E_cin = (m . v²) / 2

Lembrando que esse “m” da equação de energia cinética representa a massa relativística. Com isso, chegamos na famosa equação de Einstein: