Quadrantes no ciclo trigonométrico
Redução ao primeiro quadrante
Orientação no ciclo trigonométrico
Ângulos que ultrapassam a primeira volta
Técnicas de redução ao primeiro quadrante
Redução de quadrantes
Relembrando: Círculo trigonométrico é um círculo de raio 1 e centro na origem que possui quatro quadrantes.
Em cada um dos quadrantes temos intervalos iguais cada um com 90° ou π/2 radianos (ou rad).
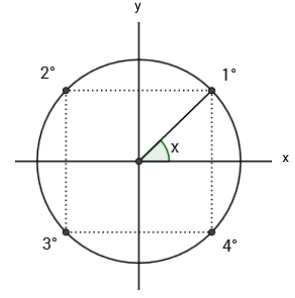
Ou seja,
- no primeiro quadrante estão os ângulos entre 0° e 90°
- no segundo entre 90° e 180°
- no terceiro entre 180° e 270°
- e no quarto quadrante entre 270° e 360°
Vimos, também, as linhas trigonométricas no ciclo:
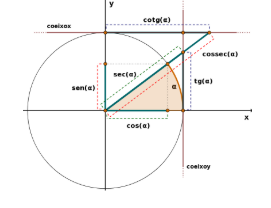
Ou seja, o cosseno é representado no eixo X e o seno no eixo Y. Com isso, podemos definir como serão os sinais nos quadrantes.
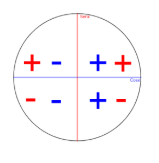
Para fazer o sinal da tangente nos quadrantes é só lembrar que
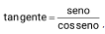
logo, basta comparar os sinais. No primeiro quadrante, ambos são positivos, então, o sinal da tangente é positivo.
Fazendo essa análise, podemos concluir que a tangente é negativa no 2° e no 4° quadrante e positiva no 1° e 3° quadrante.
Resumindo:
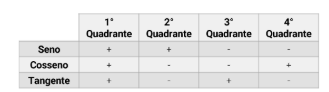
Redução de quadrante
A redução de quadrante se refere a reduzir um ângulo que não está no primeiro quadrante (maior que 90°) a um ângulo que está no primeiro quadrante
- Para reduzir do 2° quadrante para o 1°: Devemos diminuir 180° do ângulo.
- Para reduzir do 3° quadrante para o 1°: Devemos diminuir o ângulo de 180°
- Para reduzir do 4° quadrante para o 1°: Devemos diminuir 360° do ângulo.
Observe o esquema abaixo:
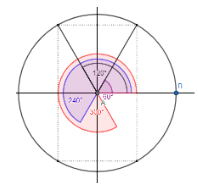
Agora que vimos como se reduz o quadrante, podemos calcular seno, cosseno e tangente de alguns outros ângulo, segundo o procedimento:
- Analisar em qual quadrante o ângulo está.
- Ver qual é o sinal da linha trigonométrica no quadrante.
- Reduzir o quadrante.