Conceito de projeção ortogonal
Questão sobre projeção ortogonal
Questão sobre projeção ortogonal em uma figura espacial
Projeção ortogonal
“A Geometria é o ramo da Matemática que se propõe a estudar as figuras existentes na natureza através das propriedades de seus elementos, definindo, caracterizando e padronizando suas formas e dimensões, facilitando assim seu próprio desenvolvimento e o de outras áreas do conhecimento científico e tecnológico.”(RABELLO, P.S.B., 2005)
“A projeção ortogonal é a representação de um objeto em um plano de projeção, quando as linhas visuais são perpendiculares a este plano.”(HOELSCHER, R.P.; SPRINGER, C.H.; DOBROVOLNY, J.S., 1978)
Definição
A projeção ortogonal das figuras geométricas sobre um plano pode ser comparada à sombra desse objeto sob a luz do sol do meio-dia.
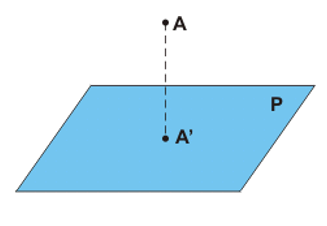
Projeção ortogonal de um ponto sobre o plano
A projeção ortogonal do ponto A sobre o plano é exatamente o ponto de encontro entre esse plano e a reta ortogonal a ele que contém o ponto A. A projeção ortográfica de um ponto num plano é sempre um ponto idêntico a ele mesmo.
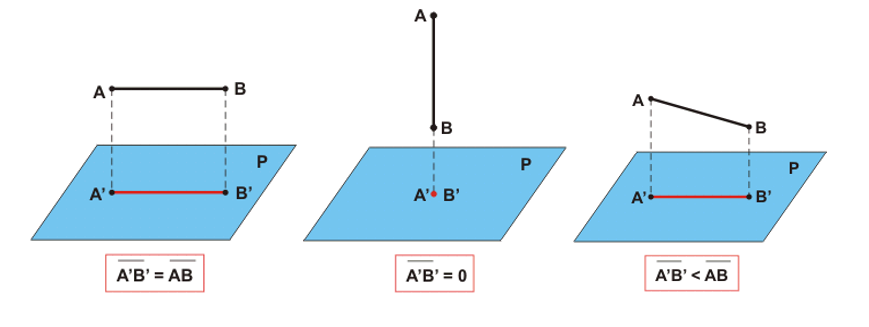
Projeção ortogonal de um segmento de reta sobre o plano
A projeção ortogonal de um segmento de reta sobre o plano pode ser um ponto ou outro segmento de reta, vai depender do ângulo que eles formam com o plano.
- Se o segmento de reta já for ortogonal ao plano (formar um ângulo de 90°), a sua projeção ortogonal será apenas um ponto.
- Se o segmento de reta não for ortogonal ao plano, sua projeção ortogonal será o segmento de reta cujas extremidades são as projeções de suas extremidades sobre o plano.
Exemplos:
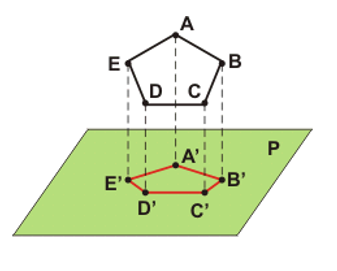
Projeção ortogonal de uma figura geométrica
Dado o plano P e a figura ABCDE, a projeção ortogonal de ABCDE sobre P será o conjunto de pontos formado pelas projeções ortogonais de todos os pontos de ABCDE sobre P.