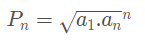Progressões Geométricas em Matemática

Progressão Geométrica

Seja a sequência numérica dada por:

(2, 6, 8, 18, 54…)

Essa sequência não é uma progressão aritmética, pois a diferença entre dois termos consecutivos não é uma constante. Contudo, podemos destacar outro padrão para essa sequência numérica, já que cada termo é o triplo do termo anterior. Essas sequências são chamadas progressões geométricas.

Chamamos de progressão geométrica, com primeiro termo igual a a​1​​ ∈ R , e a razão q ∈ R , toda sequência numérica com a seguinte lei:

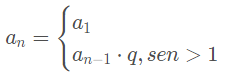
Assim, temos:

• a2 = a1 * q
• a3 = a2 * q
• a4 = a2 * q

E assim sucessivamente.

Nesse caso, a razão, representada por q, é dada por:

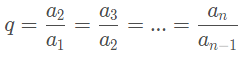
Desse modo, dizemos que uma sequência numérica é uma progressão geométrica (PG) se, e somente se, a razão entre um termo, com n > 1, e seu antecessor for uma constante.

Classificação quando ao crescimento

• Progressão geométrica crescente: a1 > 0 e q > 1
• Progressão geométrica decrescente: a1 > 0 e 0 < q < 1
• Progressão geométrica alternada: a1 ≠ 0 e 1 < 0
• Progressão geométrica constante: q = 1

Termo Geral

Seja (a1​​, a​2​​, a​3​​, …an​​) uma progressão geométrica de razão q ∈ R . Assim, para n > 1, temos:

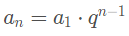
Esta é a expressão do termo geral de uma progressão geométrica calculado com base nos valores de a​1​​, q e n. Contudo, podemos determinar uma expressão para o termo geral a partir de um termo ak qualquer:

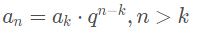
Soma dos n primeiros termos (Sn)

Dada uma PG (a1​​, a2​​, a3​​… an−2​​, an-1​​, a​n​​) cuja razão q é diferente de 1, a soma de seus n primeiros termos é representada por Sn​​, isto é:

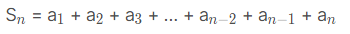
• No caso em que q = 1, então a soma dos termos da PG é igual a Sn​​ = n . a
• Para os casos em que q ≠ 1, temos:

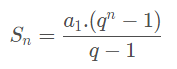
Soma dos infinitos termos (S∞ )

Para alguns tipos de progressões geométricas, podemos calcular o valor do limite da soma de seus infinitos termos. Essas sequências são chamadas de progressões geométricas convergentes e se caracterizam por ter a razão entre -1 e 1, ou seja, - 1 < q < 1. Para calcularmos a soma de seus infinitos termos, usamos a fórmula abaixo:

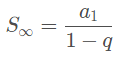
Produto dos n primeiros termos (Pn)

Dada uma PG (a1​​, a2​​, a3​​… an−2​​, a​n−1​​, an​​), podemos calcular o produto de seus n primeiros termos a partir da fórmula: