Definição
Exemplo de contagem de vértices, aresta e faces de um poliedro.
Principais relações
Exercício resolvido
Poliedros de Platão ou Regulares
Poliedros
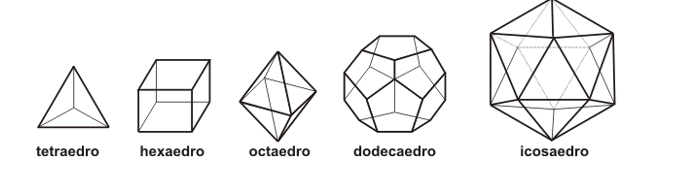
Poliedros são sólidos geométricos formados por vértices, arestas e faces, cujas superfícies são polígonos planos (triângulos, quadriláteros, pentágonos, etc.). A palavra poliedro vem do grego antigo, em que poli significa ‘’vários’’ e ‘’edros’’ significa ‘’faces’’. Veja alguns exemplos de poliedros:

Relação de Euler
Em um poliedro, como dito antes, podemos distinguir faces, arestas e os vértices. Observe abaixo:
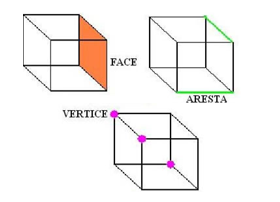
Ou seja:
- faces são as superfícies planas poligonais que limitam o poliedro.
- arestas são as interseções entre as faces do poliedro.
- vértices são os pontos de encontro das arestas
Leonhard Euler foi um matemático suíço que desenvolveu uma expressão matemática que descreve a relação entre o número de vértices, arestas e faces de um poliedro convexo. Eis a fórmula:
V + F = A +2
Devemos ter cuidado ao usar essa fórmula, pois ela funciona para qualquer poliedro convexo e para alguns poliedros côncavos. Mas o que são poliedros convexos e côncavos?
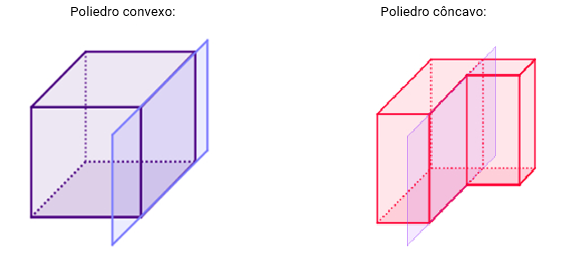
Um poliedro é chamado convexo quando o plano que contém cada face deixa todas as outras em um mesmo semiespaço.
Cálculo para quantidade de arestas de um poliedro
Seja um poliedro com f3, triangulares, f4 faces faces quadrangulares, f5 pentagonais etc.
Podemos calcular a quantidade de arestas (A) desse poliedro usando a fórmula:
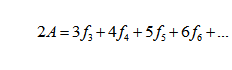
Poliedros de Platão
O filósofo Platão criou um teorema que nos diz que existem 5, e apenas 5, poliedros regulares. Esses 5 poliedros são chamados poliedros de Platão. Para que possa ser um poliedro de Platão, é necessário que o poliedro obedeça às seguintes disposições:
- todas as faces devem ter a mesma quantidade n de arestas;
- todos os vértices devem ser formados pela mesma quantidade m de arestas
Estes são os poliedros de Platão: