Polias e força elástica2 em Física

Polia fixa e Polia móvel

No dia a dia, você pode encontrar polias em academias ou ate em obras. O objetivo desse instrumento é redirecionar a força que precisa ser aplicada. Graças e esse instrumento que o pedreiro consegue fazer um saco de areia levantar puxando uma corda para baixo. Imagine um sistema com uma polia igual ao da figura 2.

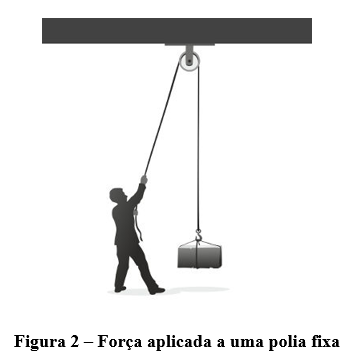
Se o homem desejar manter a caixa em equilíbrio (lembre-se que equilíbrio é aplicar força resultante = 0) é necessário que todas as forças existentes na caixa se equilibrem. Para isso, temos a força peso da caixa em equilíbrio com a tração aplicada pelo fio.

T = P

Note que, como é o homem que esta puxando a corda, a força de tração aplicada pela corda é a força que o homem faz para puxar a corda. Logo:

F = P

Esse é um exemplo de polia fixa, onde essa polia fica presa em uma estrutura e só rotaciona. Mas podemos também ter um sistema com polias moveis como é o caso da figura 3.

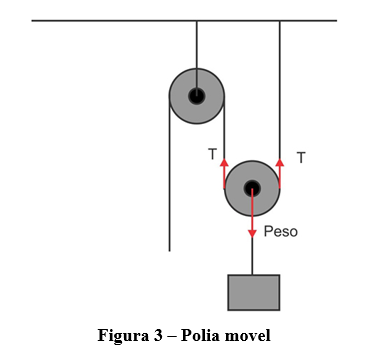
Diferente da polia fixa, onde o objetivo é apenas redirecionar (mudar direção e sentido) a força a ser aplicada, o objetivo da polia móvel é diminuir o modulo da força necessária para deixar um peso em equilíbrio (alem de redirecionar a força). Para entender isso bem, imagine que alguém puxa a corda da figura 4 com o objetivo de deixar o bloco cinza em equilíbrio.

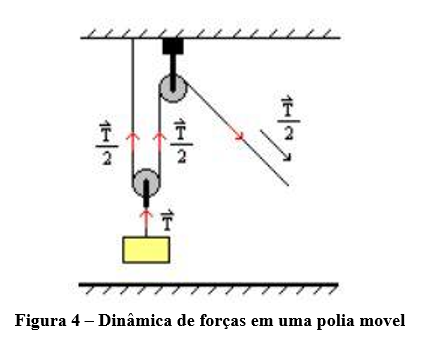
Ao puxar a corda, você aplica uma força para mover a roldana móvel e esse movimento levantar o peso. Note que como a roldana móvel apresenta dois fios: um conectado a roldana fixa e outro ao teto. Por conta disso, a força peso se equilibra com a tração dos dois fios, fazendo com que parte da força vá para a pessoa que exerce a força e a outra parte seja feita pelo teto. Para a situação da figura 4 podemos dizer que a força que a pessoa precisa aplicar para levantar um corpo é de:

F = P/2

Essa formula esta presa a situação da figura 4, onde temos apenas uma roldana móvel, mas podemos montar uma expressão generalizada para poder encontrar o valor da força para qualquer numero de roldanas.

F = P/2ⁿ

Sendo “n” o numero de roldanas móveis que o sistema apresenta.

Força elástica

Já brincou com um carrinho de fricção? Aquele que você puxa para trás e ele sai varado para frente?

Esse carrinho funciona com uma mola dentro dele capaz de coloca-lo em movimento. Isso acontece por que ao deformar uma mola, você aplica uma força chamada força elástica.

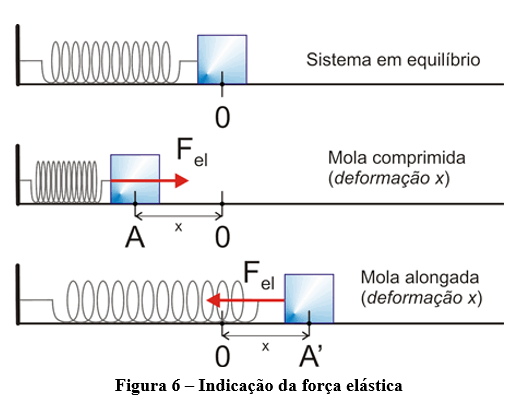
Como pode ser visto na figura 6, a deformação da mola provoca uma força elástica na direção e sentido oposto. Isso significa que se você comprime ou alonga uma mola, vai aparecer uma força para coloca-la de volta em seu estado natural (equilíbrio).

Essa força pode ser equacionada da seguinte forma:

F_el = k.x

Sendo:
• k = constante da mola (unidade = N/m)
• x = deformação da mola (unidade = m)

Associação de molas em paralelo

No caso do carrinho de fricção nos pensamos em colocar uma mola que seja capaz de movimentar o carrinho, mas nada impede de colocar mais de uma. Caso você coloque duas ou mais, você precisa ter em mente como você vai colocar essa mola, já que agora você tem uma associação de molas.

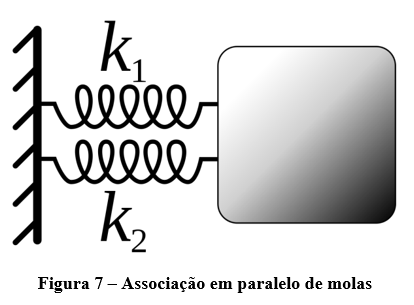
Associação em paralelo consiste em ligar molas igual a da figura 7. Dessa forma, temos que as molas conseguem junta interagir com o corpo de forma que uma não influencie diretamente na deformação da outra. Como escrito na figura 7, vamos imaginar que cada mola apresente sua própria constante “k”. Para descrever uma força elástica resultante “F_elR​​”, temos:

F_elR = F_el1 + F_el2
k_e.x_T = k₁.x₁ + k₂.x₂

Quando deformamos uma associação de molas em paralelo, todas as molas deformar da mesma forma. Logo:

k_e = k₁ + k₂

Em caso de uma associação em paralelo de “n” molas, podemos escrever da seguinte forma:

k_e = k₁ + k₂ + ... + k_n

Associação de molas em série

Já uma associação de molas em série consiste grudar uma mola em uma outra, como pode ser visto na figura 8.

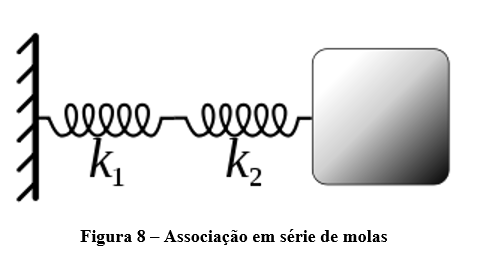
Diferente da associação em paralelo, notamos que agora a deformação de uma mola influencia diretamente na deformação da outra mola. Antes de descrever uma força elástica resultante “F_eF​e​​_l​l​​_R​R​​”, podemos constatar que a deformação total desse conjunto pode ser entendida da seguinte forma:

x_T = x₁ + x₂

Já que a força elástica é descrita como F_elF​e​​l = k . x, podemos descrever uma força elástica resultante “F_eF​e​​_l​l​​_R​R​​” da seguinte forma:

F_elR / k_e = F_el1 / k₁ + F_el2 / k₂

Nesse tipo de associação, as forças elásticas são iguais, logo, podemos simplificar a expressão para:

1/k_e = 1/k₁ + 1/k₂

Em um caso geral, temos:

1/k_e = 1/k₁ + 1/k₂ + ... + 1/k_n