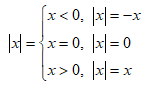Operações com números racionais em Matemática

Módulo

Denominamos de módulo de um número real, a distância deste até a origem da reta numérica.

|-a| = |+a|

Exemplos:

|-7| = 7

|π| = π

|8/5| = 8/5

|−√​2​​​| = √​2​​​

Podemos, então, dizer que

Simétrico

Dado um número real, chamamos de simétrico ou oposto dele o número que possui o mesmo módulo e o sinal oposto.

Exemplos:

• simétrico de -7 = +7
• simétrico de π = -π
• simétrico de 8/5 = -8/5

Então podemos dizer que:

simétrico de a = -a

Operações com relativos

Adição

• Sinais iguais
  repete o sinal e soma os módulos
  Ex: -7-3 = -10
• Sinais diferentes
  mantem o sinal do número de maior módulo e subtrai dele o número de menor módulo
  Ex: +9-11 = -2

Subtração

Subtrai um número é a mesma coisa que somar o simétrico dele.
Ex:
-7 - (+3) = -10
+9 - (+11) = -2

Multiplicação

• Sinais iguais
  multiplica os módulos e o sinal será positivo
  Ex: (-7).(-4) = 28
• Sinais diferentes
  multiplica os módulos e o sinal será negativo
  Ex: (-2).(+9) = -18

Divisão

• Sinais iguais
  divide os módulos e o quociente terá o sinal positivo
  Ex: (-18)/(-3) = +6
• Sinais diferentes
  divide os módulos e o quociente terá o sinal negativo
  Ex: (+20)/(-4) = -5

Propriedades

Propriedades da adição

i. Comutativa
A ordem das parcelas não altera a soma.

ii. Associativa
Quando temos mais de uma parcela, podemos associá-las de diferentes modos, sem alterar a soma.

iii. Elemento neutro
O elemento neutro da soma é zero, pois ao somar qualquer número à ele, o resultado não se altera.

iv. Elemento oposto
A soma de um número com seu oposto é igual a zero.

v. Fechamento
A soma de dois números reais é um número real.

Propriedades da multiplicação

i. Comutativa
A ordem dos fatores não alteram o produto.

ii. Associativa
Quando temos mais de dois fatores, podemos associá-los de diferentes formas.

iii. Elemento neutro
O elemento neutro da multiplicação é 1, pois multiplicando qualquer número por 1, o resultado é ele mesmo.

iv. Distributiva
O produto de um número inteiro por uma adição algébrica pode ser feito multiplicando cada termo da soma por este número e, em seguida, somando os resultados.

v. Fechamento
O produto de dois números reais, também é real.