Ondas: estacionárias e acústica em Física

Ondas estacionárioas - Cordas vibrantes

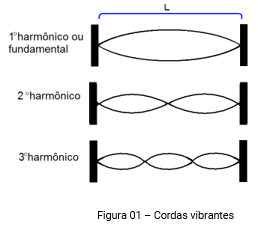
O estudo de cordas vibrantes consiste na identificação de uma coisa: Harmônicos. No estudo de harmônicos nos relacionamos esses harmônicos com parâmetros ligados a onda, como comprimento de onda, frequência, etc. Ondas em corda de comprimento L, vamos analisar como são esses harmônicos.

Na figura 01, pode-se deduzir uma fórmula para cálculo do comprimento de onda em função do comprimento da corda:

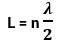
Onde:

• n é o número do harmônico.
• L é o comprimento da corda.
• λ é o comprimento de onda.

Dica: Não é preciso decorar a fórmula se você perceber que o número do harmônico representa o número de "quibes" (metade do comprimento de onda) do desenho.

Ventre e Nó

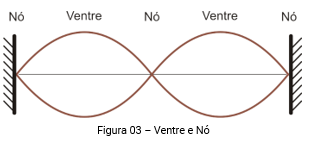
Em cordas vibrantes (e em tubos sonoros nas próximas aulas) nós podemos analisar pontos importantes em relação a interferência entre a onda emitida e a onda refletida. Esses pontos recebem o nome de Ventre e Nó. O Ventre é o ponto da onda onde ocorre interferência construtiva, ou seja, esse ponto onde a intensidade apresenta seu maior valor. Já o Nó é o ponto da onda onde ocorre a interferência destrutiva, ou seja, esse ponto onde a intensidade assume um valor nulo.

Ondas estacionárias - Tubos

Em cordas vibrantes é possível notar que todas os harmônicos observados apresentam uma coisa em comum: todos eles apresentam um nó em suas extremidades. Pode voltar para a Figura 01 para confirmar. Isso vai mudar em tubos sonoros.

Enquanto a corda vibrante representa uma corda presa em suas extremidades sendo perturbada, os tubos sonoros são tubos onde a onda sonora é confinada. Esses tubos podem ter suas extremidades abertas ou fechadas e isso interfere na forma da onda estacionara da seguinte forma:

• aberto: forma ventre
• fechado: forma nó

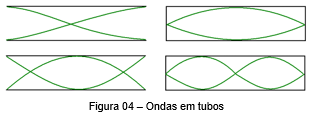
Quando esse tubo apresenta as extremidades abertas, chamamos esse tubo de tubo aberto. Para esse tubo, temos a formação de harmônicos bem parecidos com os harmônicos das cordas vibrantes (dizemos isso em relação ao número de quibes). Por conta disso, a equação que relaciona os parâmetros para tubos abertos é igual a das cordas vibrantes.

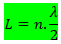
Tubos fechados são tubos que apresentam uma das extremidades fechadas. Para esses tubos vamos utilizar a mesma estratégia utilizada nas cordas vibrantes: observar a forma da onda e contar os quibes.

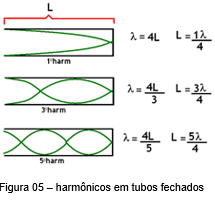
A partir das equações encontradas, podemos deduzir a seguinte equação para tubos fechados.

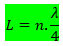Note que para tubos fechados só temos harmônicos impares.