Números Irracionais e Reais em Matemática Fundamental

Conjunto dos Números Irracionais 

Os números irracionais são números que não podem ser escritos sob a forma de fração pois são números decimais infinitos e não periódicos.Como exemplos de números irracionais podemos ter:

• π
• √2 ≈ 1,414213562…
• √5 ≈ 2,236067977…

Operações com Irracionais

Como os números irracionais são números infinitos e não periódicos, não os representamos como decimais. Assim, normalmente não efetuamos operações com números irracionais, os deixando indicados quando isso ocorre.

Exemplo: 1+√2 é uma soma que deixamos indicados por não conseguir somar ao certo esses valores.

Conjunto dos Números Racionais

O conjunto dos racionais surgiram quando houve necessidade de representar uma parte de um inteiro e é todo número da forma a/b, com b ≠ 0. Ou seja, são razões (quocientes) entre dois números inteiros. A definição formal é:

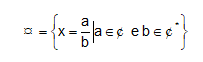
Obs: Lembrando que entre dois números racionais há infinitos números racionais.

Obs 2: Dízimas periódicas são racionais pois podem ser escritas sob a forma de fração.

Operações com Racionais

Com os números racionais, além das propriedades já vistas, adicionamos a propriedade do inverso de um número.

Exemplo: O inverso de 4 ​ = ¼

Operações entre frações

Soma e subtração

Caso os denominadores sejam iguais, bastar somar os numeradores e repetir o denominador.

Multiplicação

Multiplica-se numerador com numerador e denominador com denominador, simplificando, se possível, o resultado

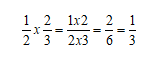
Divisão

Repete a primeira fração e multiplica pelo inverso da segunda fração.

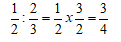
Dízima periódica

Número decimal que possui uma repetição periódica e infinita de termos (período) , mas não tem uma representação exata. São classificadas como simples e compostas:

• Simples: o período começa logo após a vírgula. Exemplo: 0,3333… , 0,121212… e 1,3333…
• Composta: Existe uma parte não periódica entre a virgula e o período: Exemplo: 0,0222…, 1,125555…