Números Complexos em Matemática

Números complexos

Os conjuntos dos números complexos é mais abrangente que o conjunto dos números reais. Esse conjunto surgiu após diversos estudos, principalmente após tentativas de se resolver equações do segundo e do terceiro grau, pois os matemáticos se depararam raízes quadradas de números negativos, que não podem ser expressas no conjunto dos números reais. Para os mais íntimos, dizemos que números complexos são números de duas dimensões. Legal, não é?

Forma Algébrica

Todo número complexo z pode ser escrito de maneira única na forma:

z = a + bi 

Com a e b pertencentes aos reais e i² = -1

Essa é a forma algébrica de se escrever um número complexo. Observe que um número complexo tem duas partes:

• Partes real: Re(z) = a
• Parte imaginária: Im(z) = b

i é a unidade imaginária, tal que i² ​​= -1; Como i² ​​= -1, podemos definir i como i = √-1

Potências de i

Usando propriedades já conhecidas de potenciação e sabendo que i = √-1, temos:

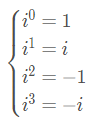
A partir da potência i⁴ as outras vão se repetindo de 4 em 4. Por isso, para calcularmos iⁿ (n um número inteiro qualquer) iremos dividir o expoente n por 4 e o resto será a potência que usaremos.

Forma trigonométrica

Plano de Argand-Gauss

Os números complexos podem ser representados de diversas formas, até aqui vimos a forma algébrica a + bi. Outra maneira de representar é em um sistema de coordenadas em um plano cartesiano. Esse sistema de coordenadas é chamado de Plano de Argand-Gauss, no eixo horizontal ficam as partes reais dos números complexos e o no eixo vertical, as partes imaginárias.
Diz-se que o ponto P (a,b) é o afixo do número complexo a + bi.

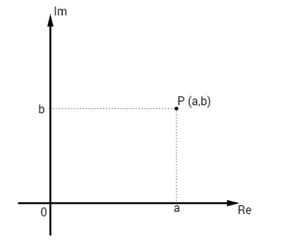
Módulo de um número complexo

O segmento de reta OP é chamado de módulo do número complexo, representado por |z| ou P. O ângulo entre o eixo Ox e o segmento OP é chamado de argumento de Z, representado por θ.

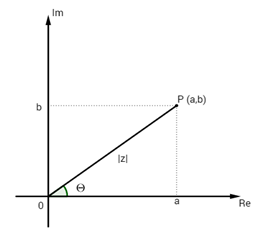
Aplicando o teorema de Pitágoras teremos:

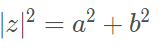
Então:

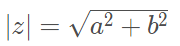
Argumento de Z

No Triângulo retângulo formado pelos vértices AOP, temos que:

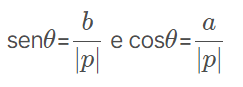
Sendo θ o argumento de Z e b = p.senθ e a = p.cosθ, podemos reescrever z = a + bi da seguinte forma:

z = p.cosθ + p.senθ.i = p(cosθ + isenθ)