Noções de Geometria Analítica: distância, perímetro, ponto médio e baricentro em Matemática

Noções de Geometria Analítica distância, perímetro, ponto médio e baricentro

Distância entre dois pontos:

Dados dois pontos A e B do plano cartesiano, chama-se distância entre eles a medida do segmento de reta que tem os dois pontos por extremidades.

1° caso: O segmento AB é paralelo ao eixo x

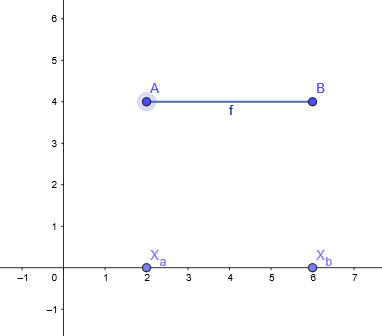
Então a distância entre A e B é dada pelo módulo da diferença entre as abscissas de A e B, isto é: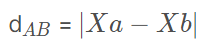

Exemplo:

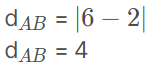
2° caso: O segmento AB é paralelo ao eixo y

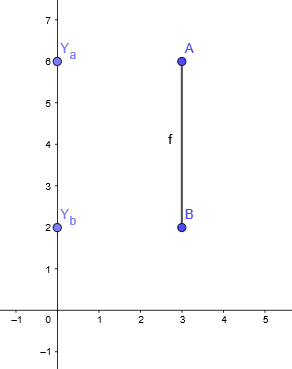
Então a distância entre A e B é dada pelo módulo da diferença entre as ordenadas de A e B, isto é:

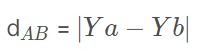
Exemplo: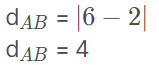

3° caso: Quando o segmento AB não é paralelo a nenhum dos eixos coordenados.

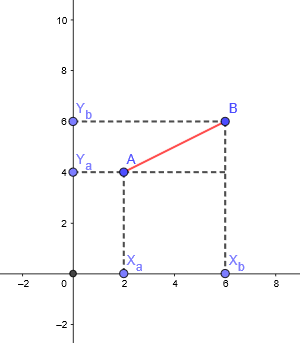
Nesse caso, podemos visualizar um triângulo que tem como hipotenusa o segmento AB. Temos então, pelo teorema de Pitágoras, a distância entre A e B dada por: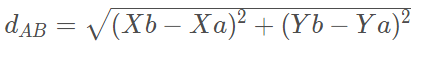

Ponto médio

Ponto médio é o ponto de equilíbrio de um segmento de reta, podemos pensar também que é o ponto localizado exatamente no meio do segmento de reta.

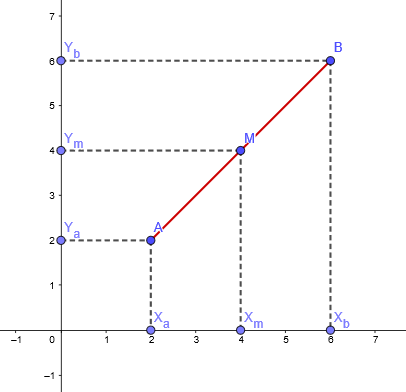
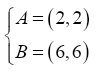
Para encontrar as coordenadas do ponto médio, tiramos a média das coordenas dos pontos A e B: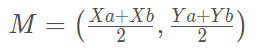

No exemplo, temos M(4,4).

Baricentro do triângulo

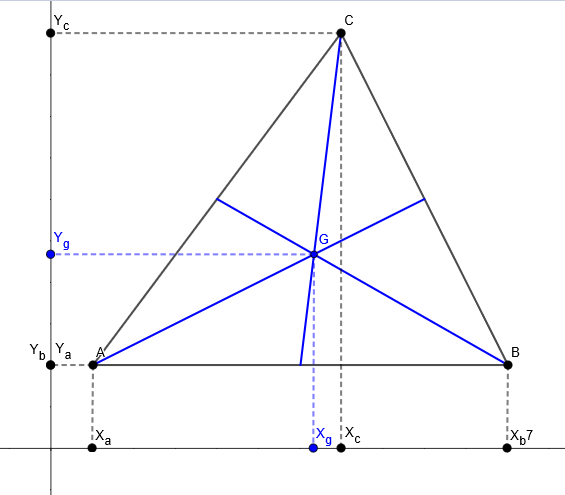
• Baricentro, também é conhecido como ponto de equilíbrio do triângulo, ele é formado pelo encontro das três medianas do triângulo, abaixo aprenderemos a encontra-lo no plano cartesiano.
  A mediana de um triângulo é um segmento de reta que liga um vétice ao ponto médio do lado oposto á esse vértice.

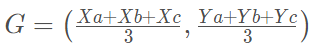
Perímetros

Perímetro de uma figura poligonal é a soma das medidas dos lados de uma figura. Logo precisamos usar os conhecimentos da distância entre dois pontos e descobrir a medida de cada lado da figura para assim
encontrar o seu perímetro.

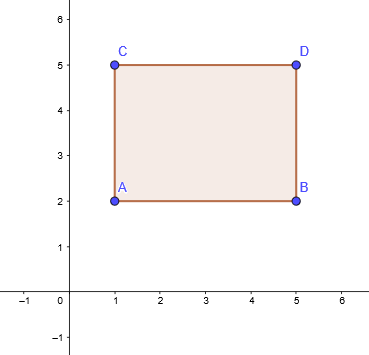
D(AB)=3

D(BC)=4

D(CD)=3

D(DA)=4

Logo o perímetro é: 3 + 3 + 4 + 4 = 14