Grandezas lineares e angulares
Ângulos em radianos e velocidade angular
Frequência e Período
Relação entre período e frequência
Relações entre grandezas lineares e angulares
Exercício sobre frequência e velocidade
Exercício sobre velocidade linear e angular
Exercício sobre rotações por segundo
Exercício sobre o tempo de um deslocamento linear
Exercício sobre as velocidades angulares dos ponteiros de um relógio
Uma partícula está em movimento circular e uniforme (MCU) quando descreve uma trajetória circular, percorrendo arcos de comprimentos (∆s) iguais em iguais intervalos de tempo (∆t), quaisquer que sejam esses intervalos. Evidentemente, a partícula em MCU também varre ângulos (∆φ) iguais em intervalos de tempo iguais.
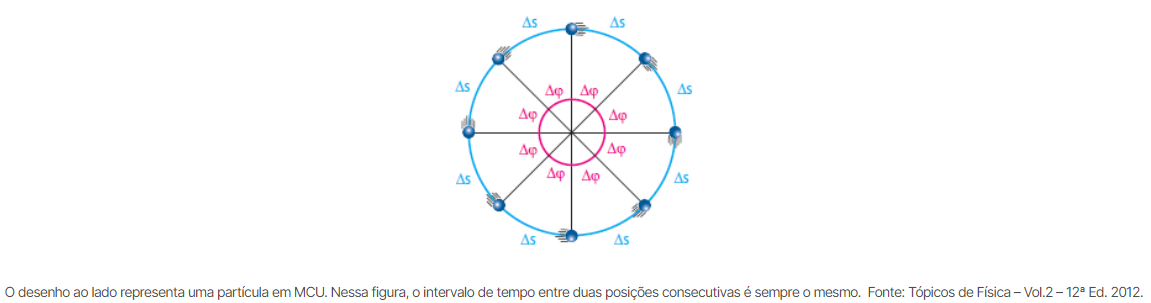
Em outras palavras, podemos escrever:
Movimento circular e uniforme (MCU) é todo movimento de trajetória circular em que a velocidade escalar, linear ou angular, é constante e diferente de zero.
v = constante ¹ 0
w = constante ¹ 0
Um exemplo importante de MCU são os movimentos de vários satélites artificiais que giram em torno da Terra:

Um satélite em órbita circular em torno da Terra realiza um movimento que, além de circular, é uniforme. Em telecomunicações, destacam-se os satélites denominados geoestacionários. Esses satélites descrevem uma circunferência com cerca de 42.000 km de raio, no mesmo plano do equador terrestre, e se mantêm permanentemente sobre um mesmo local da Terra. Assim, completam uma volta a cada 24 horas.
Período e Frequência
O MCU é um movimento periódico, isto é, todas as suas características se repetem em iguais intervalos de tempo. Cada intervalo corresponde ao tempo que a partícula leva para completar uma volta. Esse tempo denomina-se período do MCU e é simbolizado por T.
Período (T) de um MCU é o intervalo de tempo decorrido durante uma volta de uma dada partícula.
Outra grandeza referente ao MCU é a frequência, simbolizada por f.
Suponha, por exemplo, que uma partícula complete uma volta em 0,1 s. Esse valor é o período (T) do movimento. Quantas voltas ela completa na unidade de tempo, no caso, 1 s? Efetuando o cálculo, percebemos que ela completa dez voltas por segundo.
Dizemos, então, que essa é a sua frequência (f): f = 10 voltas/s
Assim, definimos:
A frequência (f) do movimento circular e uniforme executado por uma partícula é o número de voltas que essa partícula efetua por unidade de tempo. Assim, se a partícula efetua n voltas durante um intervalo de tempo Dt, sua frequência é dada por:
f = n / Δt
Unidades:
Período [T] = s
Frequência [f] = Hz = s-1 = 1 rps (rotações por segundo).
Na prática, é muito comum medir frequência em rotações por minuto (rpm). Para fazer conversões entre as unidades rpm e Hz, podemos usar a seguinte relação:


Relação entre período e frequência
Para relacionar a frequência com o período, lembre-se de que:
f = n / Δt
Se, nessa expressão, fizermos ∆t igual a um período (T), o número de voltas (n) será igual a 1. Assim, teremos:
f = n / Δt = 1 / T
f = 1 / T
Concluímos, então, que a frequência é igual ao inverso do período. Note que isso já era esperado, pois, quanto mais tempo demora uma volta (maior período), menos voltas são completadas numa unidade de tempo (menor frequência).

Função horária do espaço angular
Considere uma partícula em movimento circular uniforme (MCU). Seja φ0 seu espaço angular inicial ou fase inicial, isto é, o espaço angular ou fase no instante t0 = 0. Seja φ seu espaço angular ou fase num instante t qualquer.
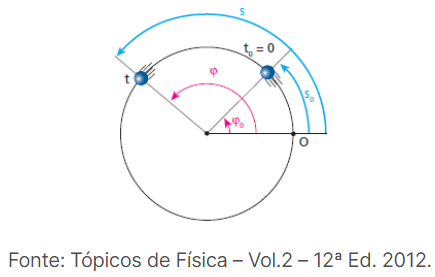
No MCU, a velocidade escalar média angular e a instantânea têm sempre o mesmo valor. Assim, podemos escrever, no intervalo de t0 a t:

A expressão que acabamos de obter é a função horária do espaço angular. Observe que ela é muito parecida com a função horária do espaço linear, que, evidentemente, continua válida e é dada por: s = s0 + v t.
A função horária do espaço angular pode ser obtida a partir da função horária do espaço linear, dividindo-se todos os termos desta última pelo raio (R) da circunferência. De fato, sendo: s = s0 + v t e dividindo os termos por R:

Velocidade angular no MCU
Como já vimos, a velocidade escalar angular, tanto média como instantânea, no MCU, é dada por:
ω = Δφ / Δt
Se fizermos ∆t igual a um período (T), nesse intervalo de tempo a partícula completará uma volta e ∆φ será igual a 2π rad. Assim, teremos:
ω = Δφ / Δt = 2.π / T
ω = 2.π.f
No gráfico da velocidade escalar angular (ω) em função do tempo, a “aérea” A entre o gráfico e o eixo dos tempos, calculada do instante t1 ao instante t2, expressa o deslocamento angular ∆φ entre esses instantes:
A= ω ∆t A = ∆φ
Observe que essa propriedade é análoga àquela já usada nos Tópicos 2 e 3: no gráfico da velocidade escalar linear (v) em função do tempo, a “aérea” fornece o deslocamento linear s.