Definição de matriz
Adição, subtração e igualdade de matrizes
Multiplicação de matrizes
Matriz Transposta e Identidade
Matriz inversa
Matrizes
A matemática dispõe de um ramo da álgebra que considera números reais organizados na forma de tabela, ou seja, em linhas e colunas. A estrutura matemática estudada nesse ramo é chamada de matriz. Uma matriz organiza os números em linhas e colunas atendendo às seguintes condições.
A matriz é representada por uma letra maiúscula do alfabeto greco-romano.
As linhas e as colunas determinam as dimensões da matriz. Se expressarmos o número de linhas por m e o número de colunas por n, sua dimensão será dada por m x n.
Os números reais que ocupam as linhas e colunas são chamados de elementos da matriz. Cada elemento está posicionado em uma linha i e uma coluna j, sendo representado pela forma aij.
Os elementos da matriz ficam dispostos entre dois parênteses, ( ), ou entre dois colchetes, [ ].
A forma genérica de escrita de uma matriz é dada por:
A=(aij)m x n
É importante representar uma matriz de uma forma genérica, ou seja, representando seus elementos por suas posições ocupadas. Veja a representação de uma matriz genérica de dimensão 3 x 4.
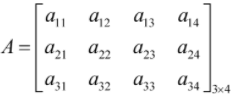
Tipos de matrizes
Matriz quadrada: é toda matriz em que o número de linhas é igual ao número de colunas.
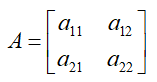
Matriz retangular: uma matriz é retangular se o número de linhas é diferente do número de colunas.
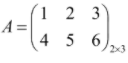
Matriz linha: uma matriz é linha se apresenta uma única linha.
A=[1 2 3 4]
Matriz coluna: uma matriz é coluna se apresenta uma única coluna.
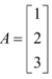
Matriz nula: uma matriz é nula quando todos os seus elementos são iguais a zero.
Matriz diagonal: uma matriz diagonal é uma matriz quadrada com todos os elementos iguais a zero, com exceção dos elementos da diagonal principal.

Matriz identidade: matriz identidade é a matriz quadrada com todos os elementos iguais a zero, com exceção dos elementos da diagonal principal, que são iguais a 1.
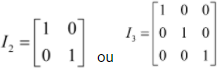
Matriz transposta:
