Equação de primeiro grau de 2 variáveis
Equação de 1 variável ≠ Equação de 2 variáveis
Montando um sistema
Método da substituição
Método da adição
Exemplos de sistemas
Sistema de equações com duas incógnitas
Uma equação com duas incógnitas poderemos ter infinitas soluções. Exemplo: x+y=10, aqui poderíamos ter como respostas (0, 10), (1, 9), (2, 8),…, e assim por diante. Para descobrirmos os valores de x e y precisamos ter no mínimo duas equações, por exemplo:
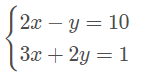
Se substituirmos o x = 3 e o y = - 4, temos:
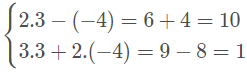
Obtemos os resultados da igualdade, logo (3, - 4) é a solução deste sistema.
A solução de um sistema de equações sempre será um par ordenado (x, y) que ao substituir no sistema satisfaz as duas equações.
Método da substituição
Solução de sistemas pelo método da substituição:
Passo 1: Escolher uma incógnita em uma das euqações e calcular seu valor algébrico.
Passo 2: Substituir o valor algébrico da incógnita na outra equação.
Passo 3: Calcular o valor numérico de uma das incógnitas.
Passo 4: Substituir o valor numérico de x em qualquer uma das duas equações e encontrar o valor numérico de y.
Exemplo:
1. Encontre a solução do sistema a seguir:
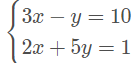
Escolhi a incógnita y na 1ª equação:
3x – y = 10→ -y =10 - 3x→ y = 3x - 10
Substituindo na segunda equação esse valor algébrico de y.
2x + 5y = 1→ 2x + 5. (3x- 10) = 1→ 2x = 15x – 50 = 1 → 17x = 51 → x = 3
Após encontrar o valor numérico de x, escolha uma das equações para cumprir o quarto e último passo: obter o valor numérico de y. Escolhemos, para isso, a primeira equação.
Observe:
2x + 5y = 1 → 2 . 3 + 5y = 1 → 5y = 1 - 6 → 5y = -5 → y = -1
A solução desse sistema é S = {3, -1}
Método da adição
Este método é bem eficaz em sistemas lineares 2x2:
Passo 1: Escolher uma incógnita e multiplique sua equação pelo valor numérico da mesma incógnita em outra equação.
Passo 2: Faça o mesmo na outra equação escolhida, mas agora multiplicando pelo valor numérico da incógnita da primeira equação.
Passo 3: Soma essas duas equações.
Passo 4: Após encontrar o valor de uma incógnita, volte em qualquer uma das duas equações originais e substitua o valor encontrado para encontrar o valor da outra incógnita.
Exemplo:
2. Resolva o sistema linear a seguir pelo método da adição.
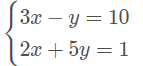
Escolhi a incógnita y, então, vou multiplicar uma pela outra.
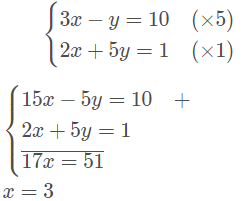
Volto para qualquer uma das equações originais e substituo o valor de x = 3.
3x - y = 10 → 3 . 3 – y = 10 → - y = 10 – 9→ y = -1
S = {3, -1}