Introdução ao estudo dos conjuntos em Matemática

Introdução ao estudo dos conjuntos

Apesar de não haver uma definição formal para conjuntos, podemos entender que um conjunto é uma reunião de elementos que pertencem a um grupo em comum. Assim, já podemos entender que, para estudar conjuntos, devemos ter em mente os elementos que formam um conjunto.

Um conjunto pode ser representado de duas formas, perceba:

Através de Chaves: Quando queremos representar um conjunto por extenso, colocamos seus elementos entre chaves e assim se entende que essa reunião de elementos formam um conjunto. Exemplo: Q = {a, b, c, d}.

Através de um Diagrama: Podemos representar um conjunto através de um diagrama onde seus elementos estão presentes em seu interior. Exemplo:

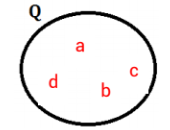
Em ambos os exemplos acima temos um conjunto Q, onde seus elementos são a, b, c e d.

Relação entre um elemento e um conjunto

Para relacionar um elemento e um conjunto, utilizamos os símbolos
∈ (Pertence) e ∉ (Não pertence).

Exemplo: Considere o conjunto Q = {a, b, c, d}. Podemos dizer que a ∈ Q, porém t ∉ Q.

Relação entre dois conjuntos

Para relacionar dois conjuntos entre si, utilizamos os símbolos ⊂ (Está contido) e ⊄ (Não está contido), ⊃ (Contém) e ⊅ (Não contém).

Exemplo: Considere o conjunto Q = {a, b, c, d}. Perceba as seguintes relações:

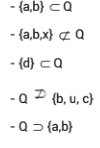
Subconjuntos de um conjunto

Um subconjunto de um conjunto Q é todo conjunto que está contido em Q. Assim, usando como exemplo o conjunto Q = { a, b, c, d}, temos que seus subconjuntos são: {}, {a}, {b}, {c}, {d}, {a,b}, {a,c}, {a,d}, {b,c}, {b,d}, {c,d}, {a,b,c}, {a,b,d}, {a,c,d}, {b,c,d} e {a,b,c,d}.

Perceba que nesse conjunto de 4 elementos, existem 16 = 2⁴ subconjuntos. Analogamente, a grosso modo, podemos dizer que num conjunto de n elementos, teremos 2ⁿ subconjuntos desse conjunto.

Quando tratamos de conjuntos, temos algumas operações que podemos efetuar entre eles.

União entre conjuntos (U): Na união entre dois conjuntos, representada pelo símbolo “U”, temos que, literalmente, unir os elementos de todos envolvidos na operação em um único conjunto só.

Exemplo: Sejam os conjuntos S = {1, 2, 3, 4} e T = {1, 3, 5, 7}, dizemos que a união S U T = {1, 2, 3, 4, 5, 7}, ou seja, todos os elementos reunidos no conjunto união.

Interseção entre conjuntos (∩): Na interseção entre dois conjuntos, representada pelo símbolo “∩”, temos que o conjunto interseção será aquele que contém todos os elementos presentes em todos os conjuntos envolvidos, ou seja, todos os elementos em comum entre os conjuntos.

Exemplo: Sejam os conjuntos S = {1, 2, 3, 4} e T = {1, 3, 5, 7}, dizemos que a interseção S ∩ T = {1,3}, ou seja, todos os elementos presentes nos dois conjuntos.

Subtração ou diferença entre conjuntos: Na subtração entre dois conjuntos, o conjunto subtração é aquele que contém os elementos do primeiro conjunto que NÃO estão presentes no segundo conjunto.

Exemplo: Sejam os conjuntos S = {1, 2, 3, 4} e T = {1, 3, 5, 7}, dizemos que a subtração S – T = {2, 4}, ou seja, o que tem em S e não tem em T. Já a subtração T – S = {5, 7}, ou seja, o que tem em T e não tem em S.

Conjunto complementar: Seja A e B dois conjuntos quaisquer com A⊂B. O conjunto diferença é chamado de complementar de A com relação a B.