Produto Cartesiano
Relação
Domínio, imagem e contradomínio
Função: definição
Interpretação gráfica
Introdução ao estudo das funções
Definição
Função é uma lei que transforma elementos de um conjunto em elementos de outro conjunto, por exemplo, ao falarmos que os valores sempre dobram, isso é uma lei, que matematicamente escrevemos como f(x) = 2x. Podemos representar uma função de forma genérica como:
f : A 🡪 B
x 🡪 y = f (x)
Ou seja, cada função que associa valores do conjunto A a valores do conjunto B e onde cada elemento x ∈ A corresponde um único y ∈ B.
Domínio, Contradomínio e Imagem
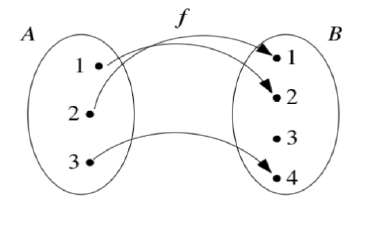
O conjunto A é denominado domínio da função, também chamado de conjunto de partida e o conjunto B é denominado contradomínio da função, ou é o conjunto de chegada. Outra forma de interpretar é que o domínio é o conjunto onde estão os valores possíveis para o x e o contradomínio é o conjunto que estão os elementos que podem corresponder aos elementos do domínio.
Já a imagem da função são todos os elementos de B que estão relacionados com os elementos de A. Ou seja cada elemento x do domínio se relaciona a um e somente um elemento y do contradomínio. Vale ressaltar que não necessariamente a imagem da função é igual ao contradomínio.
Classificação:
Função sobrejetora: É aquela que tem o conjunto imagem igual ao contradomínio.
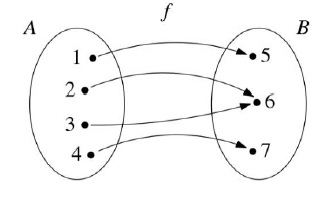
Função injetora: É aquela que, para cada elemento da imagem, existe apenas um elemento no domínio. Ou seja, em uma função injetora, elementos distintos do domínio possuem imagens distintas no contradomínio.
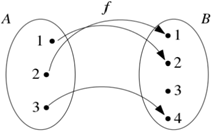
Função bijetora: Uma função é bijetora quando é simultaneamente injetora e sobrejetora.
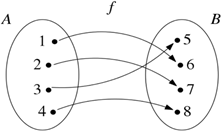
Obs: É importante saber que existem funções que não são nem injetoras e nem sobrejetoras. Elas simplesmente não apresentam classificação sob esse critério.
Função par: Uma função é dita par, se e somente se f(-x) = f(x). Ou seja, valores simétricos de x possuem a mesma imagem.
Dica: o gráfico de uma função par apresenta simetria em relação ao eixo y.
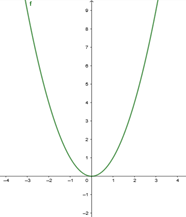
Função ímpar: Uma função é dita ímpar, se e somente se f (-x) = -f(x). Ou seja, valores simétricos de x possuem imagens simétricas.
Dica: o gráfico de uma função ímpar apresenta simetria em relação à origem.
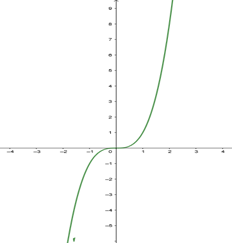
Obs: Existem funções que não podem ser classificadas quanto a paridade, ou seja, não são nem pares nem ímpares.
Restrição do domínio
Algumas funções reais apresentam problemas no cálculo de imagens para certos valores de x. A função f (x) = 3/x apresenta problema para x = 0, já que não existe divisão por zero. Como o elemento x = 0 não possui imagem, dizemos que ele não está definido no domínio dessa função. Dessa maneira, temos que prestar atenção e calcular o domínio da função com que estamos trabalhando. Temos que observar duas condições necessárias:
- O denominador de qualquer função é diferente de zero.
- Radicando de raízes de índice par são sempre positivos.
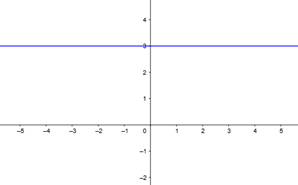
Função constante:
É aquele que, qualquer que seja o valor da abscissa, terá sempre a mesma ordenada.
Ex: f(x) = 3.
No exemplo acima fica claro que a função independe da variável x, ou seja, qualquer que seja o valor de x, a função sempre valerá 3.