Ponto, reta e plano
Grau, minuto e segundo
Operações com ângulos
Operação com ângulo: divisão
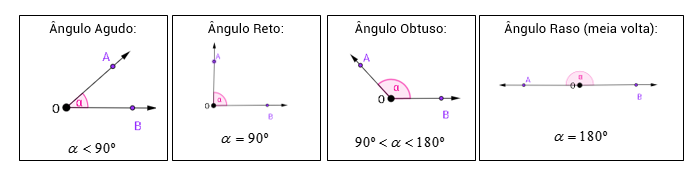
Classificação dos ângulos
Exemplificando os ângulos
Retas paralelas cortadas por uma transversal
Ângulos colaterais internos e externos
Introdução à geometria plana
Principais Conceitos
Ponto, reta e plano são elementos cuja existência é aceita sem uma definição. Suas representações são dadas por:
Ponto: representamos com letras latinas maiúsculas: A, B, C, P, …

Plano: representamos com letras gregas minúsculas: α, β, y, θ
Reta: representamos com letras latinas minúsculas: a, b, c, r, t,…
Semirreta: uma semirreta é uma das partes de uma reta limitada por um único ponto P.

Segmento de reta: dada uma reta , o segmento de reta é a parte limitada entre os pontos A e B.

Ângulo
Ângulo é a parte do plano delimitada por duas semirretas de mesma origem. Chama-se de lado as duas semirretas que formam o ângulo, e de vértice a origem comum às duas semirretas.
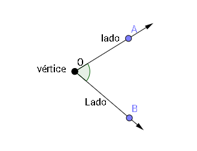
Representação AOB
Unidade de medida de ângulo: existem duas medidas angulares principais, o grau e o radiano.
- Grau: 1/360 do comprimento angular de uma circunferência. Ou seja, uma volta completa na circunferência percorre 360°.
- Radiano: Medida angular de um arco com o mesmo comprimento métrico do raio. Como a circunferência tem comprimento 2π vezes o seu raio, seu comprimento angular é 2π radianos.
2πrad ⇔ 360°
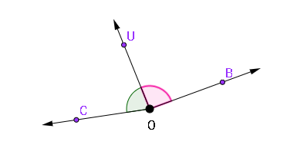
Ângulos adjacentes: dois ângulos são adjacentes se forem consecutivos e não possuírem pontos internos em comum.
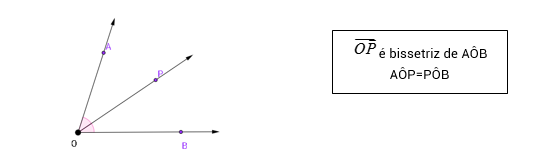
Bissetriz: divide um ângulo em dois ângulos congruentes.
Ângulos Complementares: dois ângulos que somados dão 90º.
Complemento de a é 90° – a.
α + θ = 90°
Ângulos Suplementares: dois ângulos que somados dão 180º.
Suplemento de a é 180° – a.
α + θ = 180°
Ângulos Replementares: dois ângulos que somados dão 360°.
Replemento de a é 360° – a.
α + θ = 360°
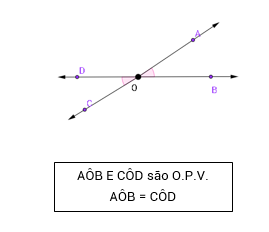
Ângulos Opostos pelo Vértice: dois ângulos serão opostos pelo vértice (O.P.V.) quando um deles for composto pelas semirretas opostas do outro.