Introdução à cinemática vetorial em Física

Na Física, temos como objetivo explicar a natureza e, para isso, fazendo diversas medições. Essas medidas podem ser grandezas escalares ou vetoriais. Vetores são grandezas que apresentam: Modulo, Direção e Sentido. Vamos entender isso melhor...

• Módulo: Representa a intensidade daquele vetor, podemos pensar nele como o número atrelado aquele vetor. Normalmente, representamos o modulo do vetor através do “tamanho” desse vetor. Assim se você encontrar um vetor grandão, é porque esse vetor tem um modulo grande.
• Direção: Representa o eixo onde esse vetor está posicionado. Inicialmente, vamos separar em duas direções: Horizontal e Vertical. Mais para frente vamos analisar vetores em diagonal e, também, vetores em direções perpendiculares (para situações em 3D). Mas calma... tudo ao seu tempo.
• Sentido: Representa o sentido para onde esse vetor aponta. Pense que dizer que um vetor está na horizontal não é o bastante, precisamos dizer se ele está apontando para esquerda ou para direita, por exemplo.

Dica: Pense que na representação vetorial (o desenho do vetor), a direção e a “traço” e o sentido e a “seta”. Isso pode ajudar a lembrar.

O objetivo dessa aula está em entender o que é um vetor e como fazer operações com esses vetores.

Operações Vetoriais

Multiplicação de um escalar por um vetor

Supondo o vetor abaixo:

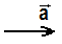
Esse vetor apresenta as seguintes características:

• Direção: Horizontal
• Sentido: Para direita
• Módulo ou intensidade: a = 1 unidade de medida (u.m.)

(para simplificar vamos escrever o módulo do vetor apenas como a.)

Dado um vetor b, vetor esse que apresenta um modulo igual a 3 vezes o modulo do vetor a. Calculando o módulo do vetor b, podemos dizer que b = 3a. Logo:

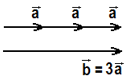
Pode-se concluir que o resultado do módulo de b vale 3 unidades.

Obs: É importante notar que quando se multiplica um vetor por um número escalar, sua direção e sentido não são alterados, porém caso o escalar seja negativo, a direção do vetor permanece a mesma, mas seu sentido será invertido.

Adição de vetores

Mesma direção e sentido

Quando efetuamos uma soma de dois vetores que apresentam a mesma direção e sentido, basta fazer a soma algébrica dos vetores.

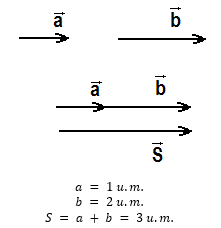
Mesma direção e sentidos opostos

Quando efetuamos uma soma de dois vetores que apresentam mesma direção, mas sentidos opostos, a soma se torna uma subtração.

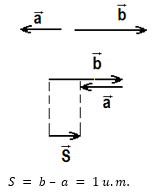
Obs: Embora a conta seja uma conta de subtração o desenho é o vetor soma. Isto acontece porque a soma vetorial não representa uma soma escalar comum. Note também que adotamos sinais para representar sentidos. O vetor b ganhou um sinal + e o vetor a ganhou um sinal -.

Direções Perpendiculares

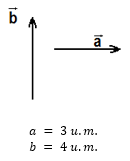
O vetor soma é dado pela junção dos vetores, sempre colocando a ponta do primeiro vetor junto do final do 2° vetor como na figura abaixo:

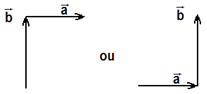
O vetor soma (S) será representado graficamente como uma seta que liga o início do 1° vetor ao final do 2° vetor. Assim:

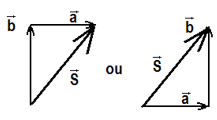
Esse método recebe o nome de regra do polígono, mas também podemos utilizar uma outra regra equivalente: A regra do paralelogramo. A regra do paralelogramo consiste em traçar retas paralelas aos vetores. Assim:

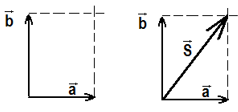
Para calcular o valor do vetor S (seu módulo) é preciso usar o Teorema de Pitágoras:

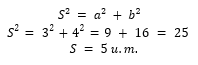
Direções quaisquer

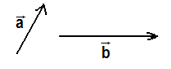
Aplicando a regra dos paralelogramos, podemos efetuar a soma vetorial dos vetores acima.

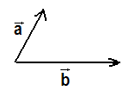
São traçadas retas paralelas aos vetores;

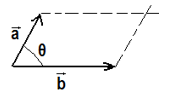
O vetor S será o vetor que tem como origem o encontro das origens dos demais vetores e como fim o encontro das retas paralelas aos vetores.

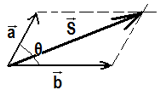
Desta forma é possível calcular o módulo de S utilizando a fórmula a seguir:

S¹ = a² + b² + 2.a.b.cosθ

Obs: Decomposição Vetorial. Fazer a decomposição é projetar o vetor em suas componentes ortogonais (eixo x e y).

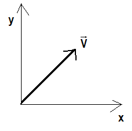
Considere um vetor v0 formando um ângulo α em relação a uma direção qualquer. Este vetor pode ser sempre decomposto em duas direções perpendiculares, sendo:

• v_0x componente de v₀ na direção x
• v_0y componente de v₀ na direção y

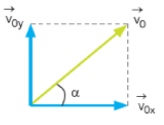
Os módulos destas duas componentes serão dados por:

• v_0x = v₀.cosθ
• v_0y = v₀.senθ

Substração de vetores

A operação de subtração de vetores pode ser feita pelas mesmas regras da adição.

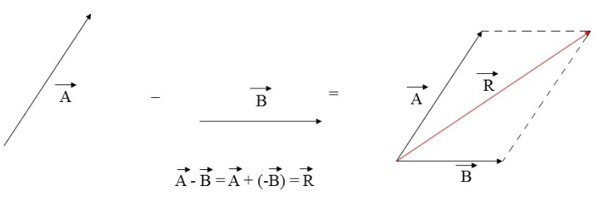
Regra do Paralelogramo

1.º Faça linhas paralelas a cada um dos vetores, formando um paralelogramo.
2.º De seguida, faça o vetor resultante, que é o vetor que se encontra na diagonal desse paralelogramo.
3.º Faça a subtração, considerando que A é o vetor oposto de -B.

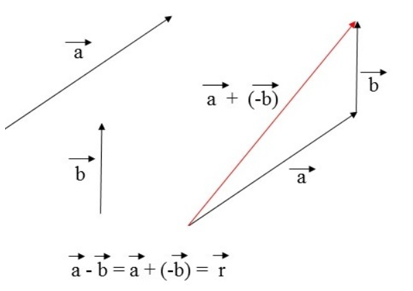
Regra do Poligonal

1.º Junte os vetores, um pela origem, outro pela extremidade (ponta). Faça assim sucessivamente, conforme o número de vetores que precisa somar.

2.º Faça uma linha perpendicular entre a origem do 1.º vetor e a extremidade do último vetor.

3.º Faça a subtração da linha perpendicular, considerando que A é o vetor oposto de -B.

Deslocamento e Distância Percorrida

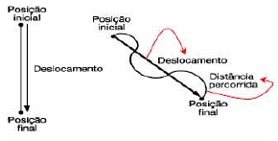
Quando falamos de transporte, precisamos ter bem claro os conceitos de deslocamento e distância percorrida, que apesar de parecerem sinônimos, não são iguais fisicamente. Quando temos um corpo em algum lugar, dizemos que ele esta ocupando uma posição ou um espaço. Com isso, vamos dizer que um móvel ocupada uma determinada posição (10) e ele vai deslocar ate outra posição (30). Como pode ser observado na imagem abaixo, que utiliza a unidade de posição em metros (m).

Na Física, nos descrevemos essas grandezas de seguinte forma:

• Posição inicial→ S₀ = 10 m
• Posição final→ S = 30 m

Com isso, podemos dizer que o móvel sofreu uma mudança (variação) de posição. Na Física, nos indicamos essa variação colocando um delta (Δ) na frente da grandeza. Logo, podemos descrever a variação da posição da seguinte forma:

ΔS = S - S₀

Descobrimos que, no exemplo feito, o móvel deslocou 20 metros. O deslocamento é uma grandeza que depende apensar da posição final e inicial do corpo que esta em movimento, independendo do caminho que esse corpo utilizou. Já a distância percorrida contabiliza esse caminho, diferenciando, no nosso exemplo, se o móvel decidiu ir de 10 m para 30 m em uma linha reta ou em um caminho sinuoso. Para entender melhor isso, observe a imagem abaixo.