Inequações trigonométricas em Matemática

Inequações Trigonométricas

Uma inequação trigonométrica é uma desigualdade, em cujas incógnitas aparecem funções trigonométricas.

Exemplo: sen(x) < ½​​

Ao trabalhar com esse tipo de inequação, normalmente é possível reduzi-la a alguma inequação conhecida, que é chamada de inequação trigonométrica fundamental. Dá uma olhada em 6 inequações fundamentais:

• sen x > n (sen x ≥ n):
  Seja n o seno de um arco y qualquer, tal que 0 ≤ n < 1. Se sen x > n, então todo x entre y e π – y é solução da inequação, assim como podemos ver na parte destacada de verde na figura a seguir:

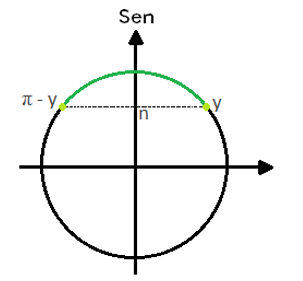
A solução dessa inequação pode ser dada, no intervalo de uma só volta, como:

S = { x 𝛜 ℝ | y < x < π – y}. Para estender essa solução para o conjunto dos reais, podemos afirmar que

S = { x 𝛜 ℝ | y + 2kπ < x < π – y + 2kπ, k 𝛜 ℤ } ou S = { x | y + 2kπ < x < (2k + 1)π – y, k 𝛜 ℤ }

• sen x < n (sen x ≤ n)
  Se sen x < n, então a solução é dada por dois intervalos. A figura a seguir representa essa situação:

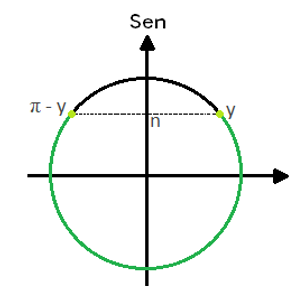
Na primeira volta do ciclo, a solução pode ser dada como S = { x 𝛜 ℝ | 0 ≤ x ≤ y ou π – y ≤ x ≤ 2π} . No conjunto dos reais, podemos afirmar que
S = { x 𝛜 ℝ | 2kπ ≤ x < y + 2kπ ou π – y + 2kπ ≤ x ≤ (k + 1).2π, k 𝛜 ℤ }.

• cos x > n (cos x ≥ n)
  Seja n o cosseno de um arco y, tal que – 1 < n < 1. A solução deve ser dada a partir de dois intervalos:
  0 ≤ n < 1 ou – 1 < n ≤ 0.
  Veja a figura a seguir:

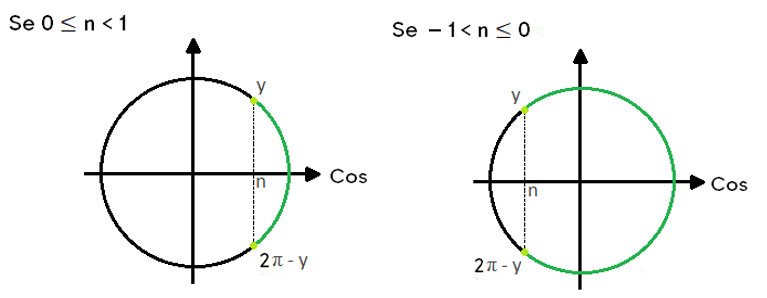
Para que a solução dessa inequação esteja na primeira volta do ciclo trigonométrico, devemos apresentar
S = { x 𝛜 ℝ | 0 ≤ x < y ou 2π – y ≤ x < 2π }. Para estender essa solução para o conjunto dos reais, podemos dizer que S = { x 𝛜 ℝ | 2kπ ≤ x < π + 2kπ ou 2π – y + 2kπ < x < (k + 1).2π, k 𝛜 ℤ }.

• cos x < n (cos x ≤ n)
  Nesses casos, há apenas um intervalo e uma única solução. Observe a figura a seguir:

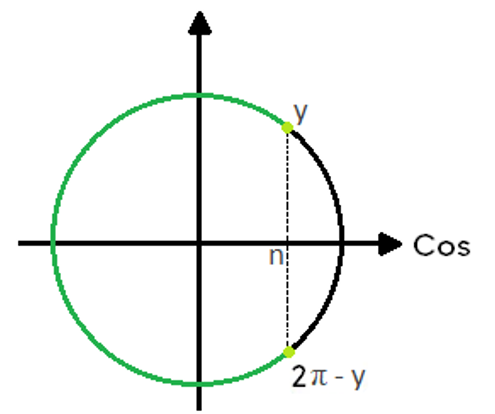
Na primeira volta do ciclo, a solução é S = { x 𝛜 ℝ | y < x < 2π – y}. No conjunto dos reais, a solução é
S = { x 𝛜 ℝ | y + 2kπ < x < 2π – y + 2kπ, k 𝛜 ℤ}.

• tg x > n (tg x ≥ n)
  Seja n a tangente de um arco y qualquer, tal que n > 0. Se tg x > n, há duas soluções como podemos ver na figura:

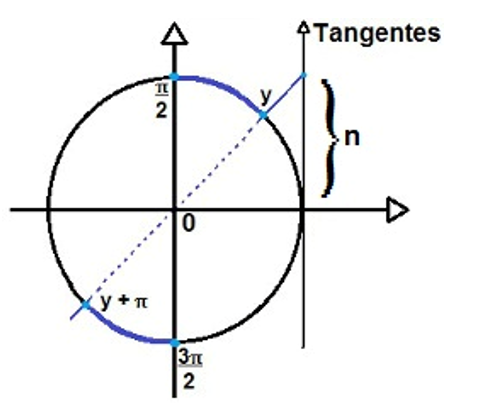
A solução dessa inequação pode ser dada no conjunto dos reais como S = { x 𝛜 ℝ | y + 2kπ < x < π/2 + 2kπ ou y + π + 2kπ < x < 3π/2 + 2kπ}. Na primeira volta do ciclo, temos: S = { x 𝛜 ℝ | y < x < π/2 ou y + π < x < 3π/2, k 𝛜 ℤ }.

• tg x < n (tg x ≤ n)
  Esse caso é semelhante ao anterior. Se n > 0, temos:

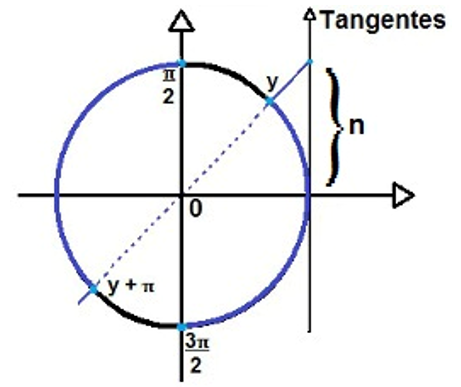
Na primeira volta do ciclo, temos como solução: S = { x 𝛜 ℝ | 0 ≤ x < y ou π/2 < x < y + π ou 3π/2 < x < 2π}. No conjunto dos reais a solução é S = { x 𝛜 ℝ | kπ ≤ x < y + kπ ou π/2 + kπ < x < (k + 1).π, k 𝛜 ℤ }.