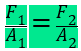Hidrostática em Física

Massa específica ou densidade absoluta (µ)

Sejam m1, m2, ..., m_n as massas de porções de uma substância pura em uma mesma temperatura e submetida à mesma pressão. Sendo V1, V2, ..., V os respectivos volumes, podemos verificar que:

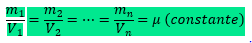
Por definição, a constante m é a massa específica ou densidade absoluta da substância.

Do exposto, concluímos que: Em pressão e temperatura constantes, uma substância pura tem massa específica (m) constante e calculada pela divisão da massa considerada (m) pelo volume correspondente (V):

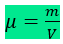Unidade (SI): [ µ ] = kg/m³

Densidade do corpo (d)

Por definição, a densidade de um corpo (d) é o quociente de sua massa (m) pelo volume delimitado por sua superfície externa (V_ext):

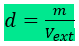
Densidade relativa

Por definição, chama-se densidade de uma substância A relativa a outra B o quociente das respectivas massas específicas das substâncias A e B quando à mesma temperatura e pressão:

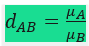
Se os volumes das substâncias consideradas forem iguais (V_A = V_B = V), teremos:

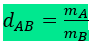Observe que a densidade relativa, por ser definida pelo quociente de grandezas medidas nas mesmas unidades, é uma quantidade adimensional.

Pressão

É a grandeza escalar que corresponde à razão entre a resultante perpendicular (normal) das forças e sua área de atuação.

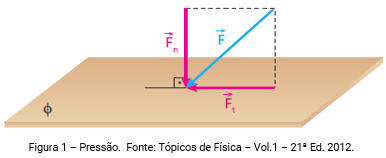
Por definição, a pressão média (p_m) que F exerce na superfície φ é obtida dividindo-se o módulo da componente normal de F em relação a f (Fn) pela correspondente área A:

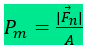Convém destacar que apenas e tão somente a componente normal da força exerce pressão na superfície. A componente tangencial exerce outro efeito, denominado cisalhamento.

Unidade (SI): N/m² = Pa (Pascal).

Obs.: 1 atm = 1.10⁵ Pa

Teorema de Stevin

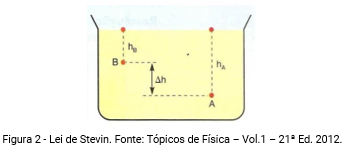
Consideremos um líquido de massa específica μ, em equilíbrio no recipiente da figura. Os pontos A e B do líquido estão situados a uma distância h_A e h_B, respectivamente, da superfície do líquido.

Pode-se mostrar que:

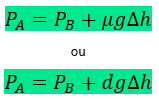
Obs¹.: Se o ponto B estiver na superfície do líquido, a pressão exercida pelo ar é a pressão atmosférica P0, e a equação acima toma a forma PA = P0 + μg∆h, onde ∆h é a altura (desnível) entre a superfície e o ponto A.

Obs².: A pressão atmosférica suporta uma coluna de 10 m de água. Isso quer dizer que uma pessoa a 20 m de profundidade tem uma pressão de aproximadamente 3 atm (1 atm do ar e 2 atm pela água).

Princípio de Pascal

O Princípio de Pascal enuncia-se da seguinte forma:

“A diferença de pressão entre dois pontos de um flúido homogêneo em equilíbrio é constante, dependendo apenas do desnível entre esses pontos. Logo, se produzirmos uma variação de pressão num ponto de um flúido em equilíbrio, essa variação se transmite a todo o flúido”

ou seja, todos os pontos do fluido sofrem a mesma variação de pressão. Uma aplicação prática é a prensa hidráulica.

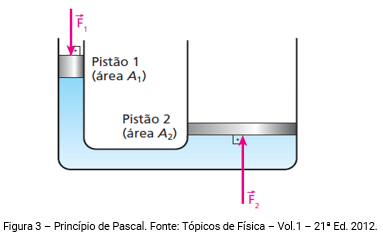
Assim, se F1 e F2 são as magnitudes das forças sobre os pistões de áreas A1 e A2, respectivamente, temos: