Função inversa: Definição
Gráfico da função inversa
Função arco seno
Função arco cosseno
Função arco tangente
O que é uma função trigonométrica inversa?
Vamos usar uma função trigonométrica como exemplo: f(x) = tg(x).
Quando pensamos em f(π/4), estamos questionando qual o valor de tg(π/4). Neste caso, tg(π/4) = 1.
Agora quando estamos lidando com um função função inversa, estamos pensando "ao contrário"! Agora, fazer f(1) siginifica questionar que ângulos têm tangente igual a 1.
Assim, funções trigonométricas fornecem como imagem o valores dos arcos que possuem determinados senos, cossenos e tangentes.
Para auxiliar nas nossas análises, recordemos os valores de senos, cossenos e tangente de determinados arcos:
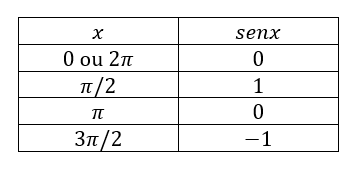
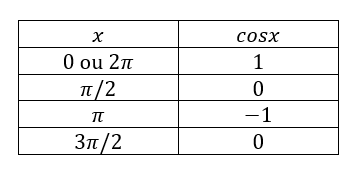
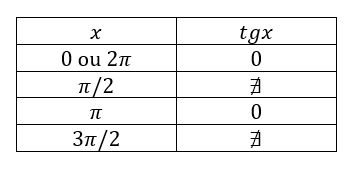
Com esses valores, iremos construir os gráficos das funções trigonométricas inversas pensando "ao contrário". Isto é, os valores de x passarão a ser a imagem da função, enquanto que os valores de sen(x), cos(x) e tg(x) serão o domínio da função!
Caso você queria relembrar mais sobre as funções f(x) = senx, g(x) = cosx e h(x) = tgx, acesse: Funções Seno, Cosseno e Tangente.
Função f(x) = arcsen(x)
- Função inversa à f(x) = senx.
- Quais os arcos que possuem seno igual a x?
- Gráfico:
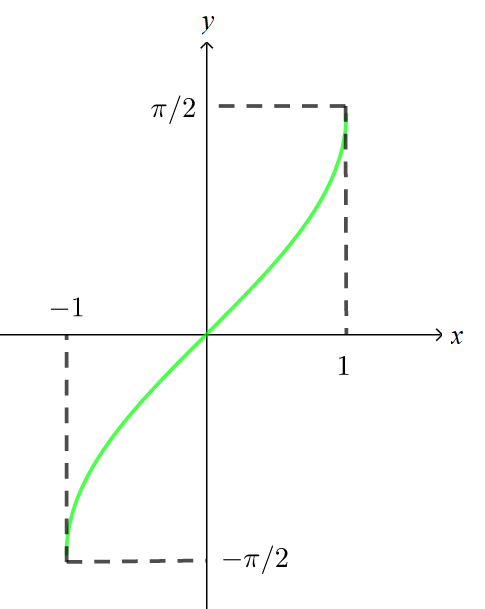
Função f(x) = arccos(x)
- Função inversa à f(x) = cosx.
- Quais os arcos que possuem cosseno igual a x?
- Gráfico:
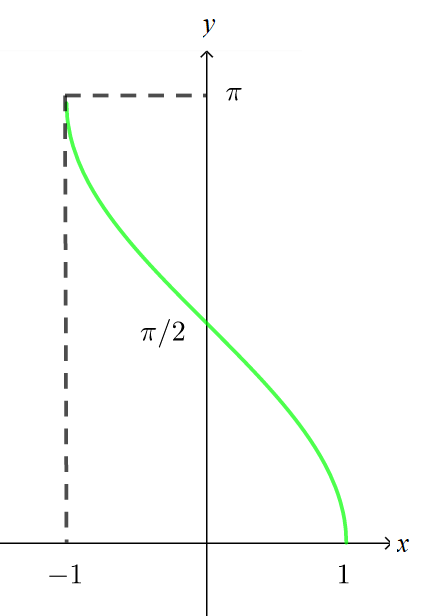
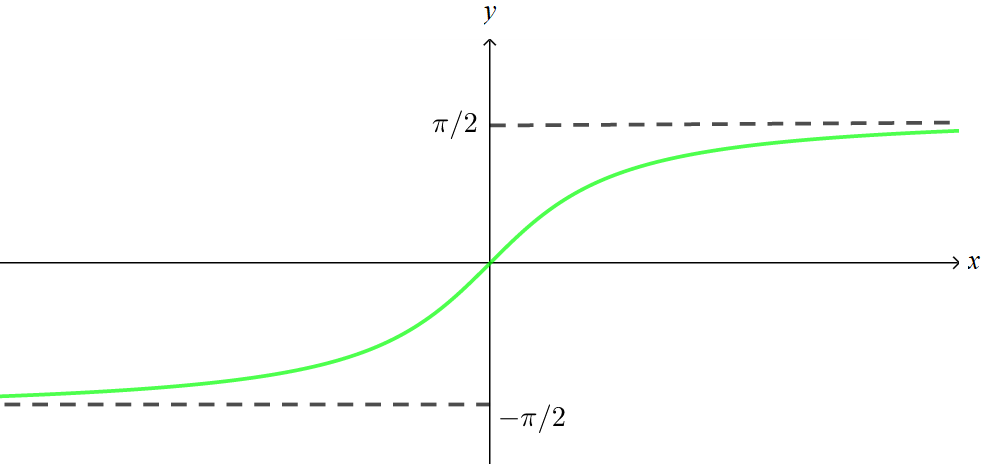
Função f(x) = arctg(x)
- Função inversa à f(x) = tgx.
- Quais os arcos que possuem tangente igual a x?
- Gráfico: