Função quadrática: estudo do sinal e problemas de máximo e mínimo em Matemática

Estudando o sinal de uma função quadrática

O que significa estudar o sinal de uma função?

Significa avaliar quando a função possui valores positivos ou negativos.

• Uma função possui valor positivo quando a coordenada y de seus pontos é positiva. Ou seja, quando seu gráfico está acima do eixo x.
• Uma função possui valor negativo quando a coordenada y de seus pontos é negativa. Ou seja, quando seu gráfico está abaixo do eixo x.

Aqui, nos preocuparemos em avaliar o sinal de uma função do segundo grau, do tipo f(x) = ax² + bx + c, cujo formato do gráfico é o de uma parábola. 

Para avaliar o valor de uma função, precisamos somente do esboço do seu gráfico, considerando suas raízes, o eixo x e o sinal do coeficiente a.

Observe os exemplos abaixo:

Exemplo 1: Estudo do sinal da função f(x) = 2x² - 6x - 8.

• Calculando as raízes da função para descobrir em que momentos a parábola intercepta o eixo x (usando Bhaskara ou Soma e Produto).

2x² - 6x - 8 = 0 → x' = 4 e x'' = -1.

• O coeficiente a da função é positivo (o a é igual a 2). Logo, a concavidade da parábola está para cima. 

Com essas informações, temos o seguinte esboço:

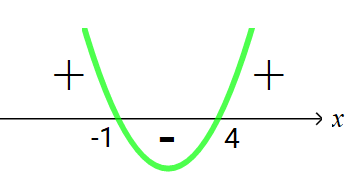
Estudo do sinal da função:

• f(x) > 0 quando x ∈ (-∞; -1) U (4; +∞)
• f(x) < 0 quando x ∈ (-1; 4)

Exemplo 2: Estudo do sinal da função g(x) = -2x² + 6x + 8.

Calculando as raízes da função para descobrir em que momentos a parábola intercepta o eixo x (usando Bhaskara ou Soma e Produto).

-2x² + 6x + 8 = 0 → x' = 4 e x'' = -1.

O coeficiente a da função é negativo (o a é igual a -2). Logo, a concavidade da parábola está para baixo. 

Com essas informações, temos o seguinte esboço:

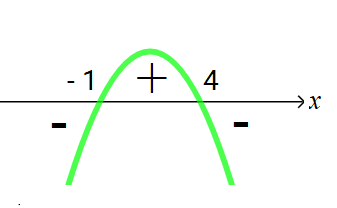
Estudo do sinal da função:

• f(x) > 0 quando x ∈ (-1; 4)
• f(x) < 0 quando x ∈ (-∞; -1) U (4; +∞)

Problemas de máximos e mínimos

Toda parábola tem um ponto de máximo ou de mínimo. No exemplo da função f(x) = 2x² - 6x - 8, visto anteriormente, perceba que ela possui uma ponto de mínimo. Já no exemplo da função g(x) = -2x² + 6x + 8, a função tem um ponto de máximo.

O pontos de máximo e mínimo também são chamados de vértice da parábola, tendo coordenadas Xv e Yv. Observe um exemplo:

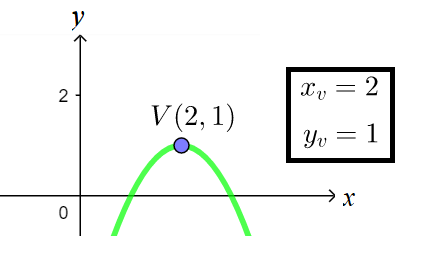
Existem fórmulas para determinarmos as coordenadas x e y do vértice. Sendo a função do tipo f(x) = ax² + bx + c, as coordenadas do vértice serão:

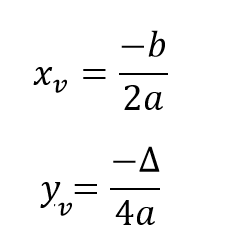
Onde ∆ = b² - 4ac.