Função ou distribuição de probabilidade em Matemática

Probabilidade - conceitos iniciais

• Experimento Aleatório: É todo aquele que o resultado é imprevisível como, por exemplo, o lançamento de um dado não viciado. Podemos lançar um dado n vezes mas ainda assim não podemos ter certeza do resultado.
• Espaço Amostral: São todos os resultados possíveis do experimento aleatório. Esse conjunto é denotado por S ou Ω e também pode ser chamado como casos possíveis. No caso do dado S = {1, 2, 3, 4, 5, 6} que são as possibilidades de resultado de lançamento de um dado.
• Evento: É qualquer subconjunto do espaço amostral. Quando calculamos probabilidade, estamos querendo saber a probabilidade do evento acontecer e é representado pela letra E. Esse conjunto também é chamado de casos favoráveis. Por exemplo: Em um lançamento de dados, se o evento E forem os números pares então ele será: E = {2, 4, 6}

Dessa forma, podemos considerar que probabilidade de ocorrer o evento E é:

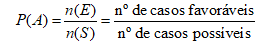
De modo que 0 ≤ p ≤1.

Ou seja, se quisermos saber a probabilidade de um lançamento de dado o número tirado ser par, a resposta seria 3/6.

Obs.: É comum a resposta vir também como uma fração irredutível, como porcentagem ou número decimal. No caso de 3/6​​, a fração irredutível seria 1/2 e em porcentagem seria 50% = 0,5.

Probabilidade complementar

Seja E um evento; então E^C​​ será também um evento que ocorrerá se, e somente se, E não ocorrer. Dizemos que E^C é o evento complementar de E e calculamos, E^C = 1 − P (E).

• Exemplo: Pense em uma sacola que possui bolinhas azuis e amarelas. Considere a probabilidade de retirarmos uma bolinha azul aleatoriamente da sacola igual a 1/4. Assim, a probabilidade de não retirarmos uma bolinha azul (isto é, de retirar uma amarela) será igual a 1 - 1/4 = 3/4.

Probabilidade da união de eventos

Sejam A e B dois eventos; então 𝐴 ∪ 𝐵 será também um evento que ocorrerá se, e somente se, A ou B (ou ambos) ocorrem. Dizemos que 𝐴 ∪ 𝐵 é a união entre o evento A e o evento B. Seu cálculo será como abaixo:

• Exemplo: Ao retirar uma carta de um baralho de 52 cartas, qual é a probabilidade de que essa carta seja vermelha ou um ás?

Seja o evento A: carta vermelha e B: a carta de ás, temos que num baralho de 52 cartas, teremos

𝑛(𝐴) = 26 (número de cartas vermelhas)
𝑛(𝐵) = 4 (número de cartas de às)
𝑛(Ω) = 52 (espaço amostral, que é o total de cartas)

Fazendo as probabilidades, temos:

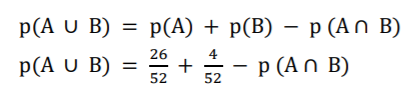
Calculando a interseção dos eventos 𝐴 e 𝐵:

𝑛(𝐴 ∩ 𝐵) = 2 (número de cartas vermelhas que são ases)

Então a probabilidade é:

Probabilidade da interseção de eventos

Sejam A e B dois eventos; então 𝐴 ∩ 𝐵 será também um evento que ocorrerá se, e somente se, A e B
ocorrerem simultaneamente. Dizemos que 𝐴 ∩ 𝐵 é a intersecção entre o evento A e o evento B.
Em particular, se 𝐴 ∩ 𝐵 = ∅. A e B são chamados mutuamente exclusivos.
Se A e B forem eventos independentes, temos:

p(A ∩ B) = p (A). p(B)

• Exemplo: São realizados dois lançamentos sucessivos de um dado perfeito. Qual é a probabilidade de ocorrer, nos dois
  casos, o número 5?

Evento A: ocorrência de 5 no 1º lançamento. Há 1 elemento que favorece esse evento A → p(𝐴) = 1/6

Evento B: ocorrência de 5 no 2º lançamento. Há 1 elemento que favorece esse evento B → p(𝐵) = 1/6

Calculando a probabilidade de ocorrer A e B:

p(𝐴 ∩ 𝐵) = p(𝐴) ∙ p(𝐵) = 1/6 . 1/6 = 1/36

Probabilidade Condicional

Seja um espaço amostral e consideremos dois eventos A e B. Com o símbolo P(A|B) indicamos a probabilidade do evento A, dado que o evento B ocorreu, isto é P(A|B) é a probabilidade condicional do evento A, uma vez que B tenha ocorrido. Quando calculamos P(A|B) tudo se passa como se B o espaço amostral fosse "reduzido" dentro do qual, queremos calcular a probabilidade de A. Calculamos uma probabilida condicional a partir da fórmula abaixo:

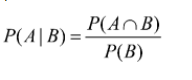
• Exemplo: Ao retirar uma carta de um baralho de 52 cartas, qual é a probabilidade de sair um ás vermelho sabendo que ela é de copas?

𝑛(Ω) = 52(total de cartas)

Evento A: sair ás vermelho. Temos 2 ás vermelhos no baralho.

Evento B: sair copas. Temos 13 cartas de copas no baralho

Evento (𝐴 ∩ 𝐵): ás de copas. Temos 1 carta dessa no baralho.

Assim, temos: