Definição: Função do 1° grau
Coeficiente Angular e Coeficiente Linear
Gráfico da função do 1° grau
Estudo do sinal da função
Ponto de encontro entre duas retas
Função Afim
Uma função f: R→R chama-se função afim quando existem dois números reais a e b tal que f(x) = ax + b, para todo x ∈ R.
Exemplos:
f(x) = 2x + 5
f(x) = -x + 2
f(x) = 1/3 x
Função Linear
Seja f: R→R definida por f(x) = ax, para todo x ∈ R.
Exemplos: f(x) = 3x, g(x) = -5x.
Função Constante
Seja f: R→R definida por f(x) = b, para todo x ∈ R.
Exemplos: f(x) = 3, g(x) = -2.
Função Identidade
Seja f: R→R definida por f(x) = x, para todo x ∈ R.
Coeficiente/Taxa de variação
Na lei da função f(x) = ax + b, o coeficiente a é chamado de coeficiente ou taxa de variação da função. Podemos calcular o valor do coeficiente angular como:
a = tgθ ou a = △y/△x
Em que θ é o ângulo que a reta da função faz com o eixo x, no sentido anti-horário.
Exemplo:
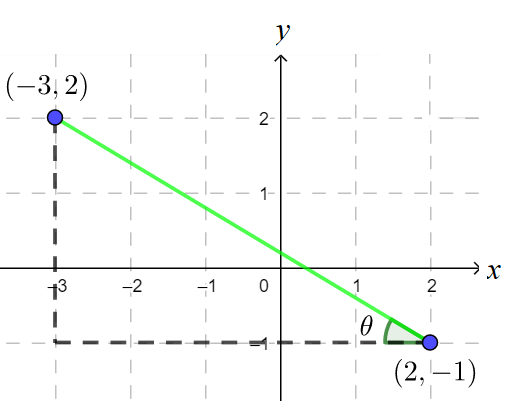
a = tgθ = △y/△x = [2 - (-1)] / (-3 - 2) = 3/-5.
Logo, o coeficiente angular (a) vale -3/5.
Coeficiente linear
Na lei da função f(x) = ax + b, o coeficiente b é chamado de coeficiente linear da função. Ele é encontrado com o valor no qual o gráfico da função intercepta o eixo y.
Exemplo:
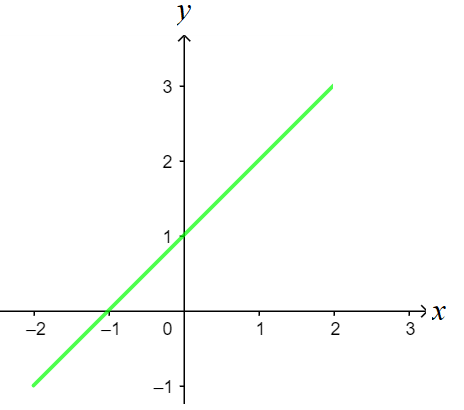
Aqui, a interção com o eixo y ocorre na altura de y = 1. Logo, o coeficiente linear da função acima será igual a 1.
O gráfico da Função Afim
O gráfico da função afim é uma reta e ela pode ser crescente (caso a taxa de crescimento seja maior que zero) ou decrescente (caso a taxa de crescimento seja menor que zero).
Exemplo de gráfico crescente:
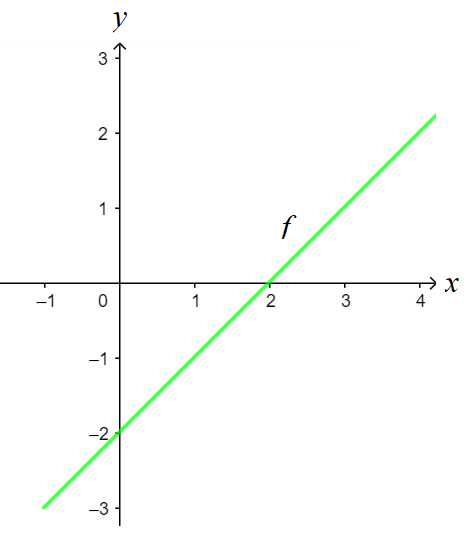
Em uma função crescente quanto maior o x, maior será o f(x). Isso ocorre quando a taxa de variação é maior que zero. Isto é a > 0.
Exemplo de gráfico decrescente:
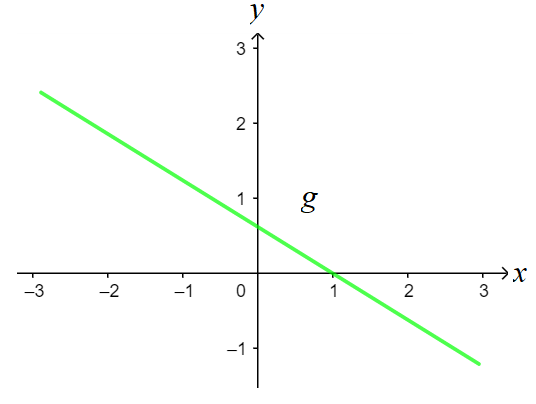
Em uma função decrescente quanto maior o x, menor será f(x). Isso ocorre quando a taxa de variação é menor que zero. Isto é a < 0.
Zero/Raiz da Função Afim
O valor de x para o qual a função f(x) = ax + b se anula, ou seja, para o qual f(x) = 0, denomina-se o zero, ou raiz, da função. No gráfico, isso representa a coordenada x da interseção com o eixo x.
Nos gráficos das duas funções anteriores, os zeros das funções eram 2 e 1, respectivamente.